6.3 区位与空间结构
6.3.1 廖什公式
区位,简单地讲就是空间位置.从本质上看,区域科学的区位,指的是出现商品或产业等的概率最大的位置,或称最可几位置.有时我们也使用区位范围一词,这时表示相应的产业或企业的产品出现在某些空间范围的概率达到了某一水平,例如它超过其它企业产品出现概率的总和.必须注意,区位(location)决不是个别的确定性的位置(site)或某个点的坐标位置,区位是统计的位置.因此说区位分析不是选址分析,后者是地理微观的.
![]()
(Location rent)学说.它定义R为经济利润,记xij为距企业iR的市场j位置,Ei是每一生产周期内企业(产业单位)的产量,Pi是单位产品i的市场价格,ai是单位产品i的生产费用,fi是单位产品的单位里程运费,廖什建议
Rij=Ei(Pi-ai)-Eifixij
(6.3.1)
当P,a,f与E无关时,有
![]()
这里fixij也可表作广义距离Cij.廖什公式可写作
Rij=(Pi-ai-Cij)Ei
(6.3.3)
廖什是区位论的集大成者,廖什公式是区位分析的基本公式.
6.3.2 杜能区位与杜能结构
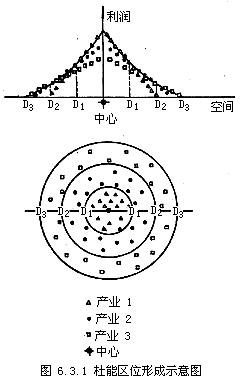
杜能设想的地域空间的地理分布是一个封闭的地域.地域是均质的同等肥沃的,中央有一个中心城市,作为农产品的市场,问空间会形成什么样的地域结构或各种产业的区位位于何处?由廖什公式容易发现这时空间划分为围绕中心的环形地带.实际上由廖什公式知距中心为x的环对给定的产业有同等的利益,故产业区必然以环的形式出现.设中心外的土地可有m种形式,则在距中心为x=D1的环上必有一种使它在这个位置上获得的利益大于m-1种,不妨记为形式1(当相等时,我们视为同种利用形式).这就是说在x<D的范围内,利用形式1出现的概率最大,按我们对区位的理解,这就是产业1的区位.随着x的增加,可能出现两种情况,其一是土地的产品量已达到中心的需求量,继续生产它会产生单位利润下降;其二是运费的增加,终于使某种单位运价较低的产品生产有大于形式1产品的利润,于是土地利用形式就转变为它种形式.以此类推,空间被利用形式划分为环形,这就是著名的杜能地域结构.由廖什公式,利益是距离的线性函数,所以某种利用形式在空间最多只能出现一次.在空间只有一个中心的情况下,当空间是均质时,出现如图6.3.1的结构,这就是典型的空间的杜能结构,环带被称作杜能环.
实际上空间不可能只有一个中心,空间也不可能是均质的,Wilson

![]()

又由廖什公式,产业k在i局域(即中心i)获得的利润为
![]()
式中,Tijk是j的产品k出现在i的概率,即相互作用测度,于是局域j的产品k的总利润为

成正比,有
![]()
这里Zj相当于上一节的Oj,上标k表示相互作用参数与产品类型有
![]()
![]()
企业在利用土地时追随最大利润.因此,Wilson和Brikin建议取下列方程描述土地的转化过程
![]()
(6.3.10)
![]()
可能性,在不考虑产业惯性时,取
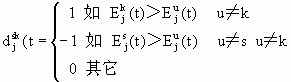
(6.3.11)
qk表示土地关于产业k的边际效应的倒数,利用这个模式Wilson和Brikin考虑了矩形空间有九个中心,沿对角线均匀分布、土地肥沃度向右下角线性递增,由上述模型计算得出的空间产业(土地利用形式)分布如图6.3.2b所示.这种土地结果仍能称为杜能型的,它的特点是市场(或被服务者)是离散分布的,资源(或服务者)是连续分布的.

通过杜能区位我们可以看出,地域结构的界线,从微观上看,过渡是概率的,从宏观上看是确定的,而由微观的概率性、实际的地域结构边界是“测不准”的.
在传统上,杜能区位被称为“农业区位”,仿佛杜能区位仅适合一个农业问题.其实不然,杜能结构被普遍地发现存在于城市的地域结构(城市的内部地区的空间格局普遍地是呈现出杜能结构).目前已经确认,城市地域可以自市中心的CBD向外,依次分为五个近环状地带:中心商务区(CBD),中心边缘区,中间居住带,城市边缘带和近郊工业区,后者具有明显的放射状特点.这时的局域呈带状(zone),在另外的空间结构中,局域可能是扇形(sector).诚然,城市地域结构模式是单中心的,如城市具备多个CBD,可能形成多中心的杜能结构.
6.3.3 霍特林-帕兰德区位与克里斯泰勒结构
Hetelling(1929)考虑了与杜能问题不同的区位问题.设想市场是连续地分布在整个空间,在空间上有两个生产同种产品的生产者,企业间两个企业应该如何选择自己生产区位,设想沿两个企业的原始位置A,B作线段AB,由廖什公式我们知在AB的垂直平分线上两个企业(设生产成本、单位运费和购价相等)获得相同的利益,越过这条平分线,在A一侧,B的利益小于A的,类似地在B一侧,A的利益小于B的.为了竞争,设A向AB的垂直平分线方向移动,这时有新的线段A′B及其垂直平分线,新平分线位于原平分线靠B的一侧.这样A夺取了B的市场,为了竞争,B也向内移动,最后两个企业的位置重合,大家共同平分整个空间市场.但是这时系统是不稳定的,不妨设A降低成本,这样在同等利润下,B的产品售价高于A的,结果是B受到彻底的排斥,B唯一的选择是离开A到一个新的位置上,利用距离近的优势,控制一个市场范围.总之,AB必然在空间有一定的距离,这个空间系统是稳定的.企业为了竞争和防止被彻底排挤出市场而在空间保持一定的距离,确定自己的生产区位,控制并趋向平分市场的过程称为Hetelling过程.
帕兰德(Palander,1935)提出了他的市场区位理论.Palander认为企业位置固定时,它在空间产生价格曲线,距离愈远,价格愈高,直到高于附近企业的价格曲线,该企业失去市场优势.
价格曲线的交点为市场区的边界,这种企业(资源)分布离散,市场分布连续的区位问题可被称为Hetelling-Palander问题,或市场区位问题.
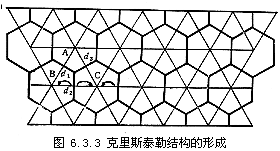
Hetelling过程直接地产生了空间的中心地结构.实际上如在企业(或城市)A,B外另有一企业或城市C出现,它的最优区位是与AB构成一个等边三角形,这样它们各占1/3的半空间.市场区位的分界线为每条边的交线,这样如图 6.3.3所示,当每个企业(中心)有同样的生产水平,市场价格不因产地而变化,空间(市场)均匀时,空间产生六边形的结构.由廖什公式在边界上相邻中心的利益相等.
中心地结构为克里斯泰勒(1933)在研究德国南部的市场地域分化时发现.故称企业(服务者、资源)离散分布,市场连续分布的地域结构为克里斯泰勒结构;中心地结构是它在空间均匀,企业均匀分布的情况下产生的特殊形式.在中心地结构中与中心配合有不同次中心组合形式,如图6.3.4所示.图6.3.4中,K=3被认为适合于商业联系,因为作用于一次中心的上级中心作用最多,说明商品交流是充分活跃和自由的.K=4时,中心城市到次中心的距离最短,适合于交通发达地区或新开发地区沿交通线的聚集.K=7中心城市对次中心控制最多,是以行政手段组织城市的适合形式,K=5可以看作K=3与K=7的过渡.
一般情况下,空间经济活动具有波动性,新的经济规模xk+1,可能依赖于前期水平xk,但前期发展也占据一部分市场,抑制后期发展.因此,在最简单情况下可设
xk+1=μxk(1-xk)
(6.3.12)
式中μ为参数.经济水平的波动,也将引起商品在市场上波动性地追逐市场,所以xk的周期也就是空间经济活动的周期,后者要求有与周期数适应的市场或中心地分布.数学上已知,随μ增加,也就是经济联系的强度的增加,(6.3.12)式的状态xk相继有2周期、4周期、3周期、5周期解,此后系统出现浑沌.市场的这种结构数与Sarkovskii周期数的对应,似乎揭示了空间结构发展的顺序是2,4,7,5,3,经济活动再加强,空间结构出现混沌.在我国西南地区,滇西经济落后地区常有7天轮流赶集的习惯,较发达地区为5天,滇东北地区传统上流行3天集市,在江南发达地区无所谓赶集,可以看作空间过程的例子.
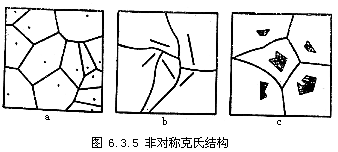
中心地结构是种理想结构,存在着两种情况破坏这种对称性.其一是地域的不均匀性,使得某些地方发展起特殊功能的城市.地域与资源的不均匀性,引发非对称的克里斯泰勒结构.Okahe和Suzuki(1987)提出在城市集合坐标给定的情况下,产品价格划一,运费价相等,则地域结构是泰森(Thiessen)多边形,如图6.3.5所示,在给定生产城市坐标为x=(x1,x2)的情况下,x属于以xi或li(线)或si(面)为中心的泰森多边形条件是生产成本Pi和运价T(di)之和达最低,即取

![]()
决定空间结构X(I).它是空间竞争达到平衡的结果.设生产成本Pi=P(常数),运输产品的单位Ci=C(常数)在这一条件下达到平衡的空间结构满足

(6.3.13)
式中,X(I)为某种空间结构,花体![]() 为可能的空间结构集合,V(xi)表示属于Vi控制范围的泰森多边形面域或市场范围,积分||xi-x||的意义是求出V(xi)范围的市场点x对xi的全部距离,这个距离与Ci之积为全部流通费用,由于Ci=C,即所有点具有同样的C,故距离||xi-x||就可代表x、xi间的流通费用.||xi-x||表示xi-x的范数,可以是欧氏距离也可以是别的度量方式.
为可能的空间结构集合,V(xi)表示属于Vi控制范围的泰森多边形面域或市场范围,积分||xi-x||的意义是求出V(xi)范围的市场点x对xi的全部距离,这个距离与Ci之积为全部流通费用,由于Ci=C,即所有点具有同样的C,故距离||xi-x||就可代表x、xi间的流通费用.||xi-x||表示xi-x的范数,可以是欧氏距离也可以是别的度量方式.
利用计算机求的(6.3.12)式仍然是困难的.它要求在可允许的结构集范围内对每一个市场点作与xi的关联,求出可能的xi-x定义的泰森多边形,从而得到![]() 全体.选择出
全体.选择出![]() 中F(X(I))最小的.一个简便的方法是水文学中常用的:连结各站点xi,作这种联结线的垂直平分线,从而获取一种以xi为中心的对空间的划分.不难理解,这种平分市场的几何方法与(6.3.12)式的计算方法完全一致,但这种方法尚不能给出图6.3.5中图b、c的结构识别.
中F(X(I))最小的.一个简便的方法是水文学中常用的:连结各站点xi,作这种联结线的垂直平分线,从而获取一种以xi为中心的对空间的划分.不难理解,这种平分市场的几何方法与(6.3.12)式的计算方法完全一致,但这种方法尚不能给出图6.3.5中图b、c的结构识别.
在前述分析中,我们总是假设,中心是同级别的,如果中心不同级别,其地域结构可能有很大变形.丁金宏在他们博士论文中提出,当空间作用中心A,B有不同的性质时,特别是相互作用核exp(-βCij)中的 Cij不仅是xi-xj的函数,而且依赖于中心xi,则不可能出现图中环状相嵌的空间结构.他认为在行政控制中,这种结构是存在的.
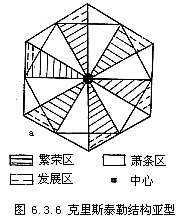

克里斯泰勒结构也普遍存在于城市地域中,它又可能有两种亚型,如图6.3.7所示.在图6.3.6a中,城市地域分化为辐射状的扇区,某些分支得到特别的发展.在6.3.6b中,城市地域形成不同层次的克里斯泰勒结构.实际上,地域结构是几种理想的空间格局的复合.
6.3.4 韦伯问题与韦伯结构
1.韦伯区位
韦伯(Weber,1909)发展了他所谓的工业区位论,韦伯理论的核心,仍然考虑孤立的区域体系,其中有一个企业,韦伯提出在区域内寻找一个最佳企业位置使企业位于资源供应和供应市场的最佳位置,使得生产、运输成本最小,从而获得最大利润.韦伯认为决定区位的因子包括一般区位因子(如劳动力费用)、特殊因子(如水质)、地方因子(地方条件)、聚集因子(如协作需要)以及自然-社会因子.实质上韦伯问题就是由离散分布的资源和市场共同决定区位.
现代区位论用廖什原理来确定韦伯区位.设生产费用(不包括原料运费等)是固定的,企业的最优位置由下式决定:
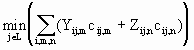
(6.3.14)
式中,j为特定的企业位置,L为可能的位置集,Yij,m为第m种产品在i点的需求量,Zij,n为第n种资源在i点的供应量,cij,m,cij,n分别为产品和资源的运价.
一般讲在资源与产品之间存在着下列技术转换关系Yij,m=wmnZij,n,因而(6.3.14)式化作
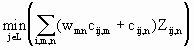
(6.3.14a)
或者记xij,k为i的第k种(广义)资源,包括市场需求与资源供应两类,则
![]()
由(6.3.14)式可以决定合适的企业位置或者说找出企业的生产区位
![]()
m是运输性因子权重.习惯上,记wn=Σmwmn.为第n种原料资源对产品的权重.设每种理论资源上只有一个供应点,n即为资源点记号,韦伯以w(n)=wn+1表地点n的区位影响,称作区位权.(6.3.14)式确定了韦伯区位过程的最优准则.实际上仅有(6.3.13)式定义的准则常不足于分析实际问题,因为资源总是有限量,资源必然受到某种总量限制,韦伯区位过程可能依赖于这种限制.
2.韦伯结构
韦伯区位过程产生韦伯地域结构.一个韦伯结构是离散的N企业对离散的N市场的控制,以Ei表示市场i的总需求,(Xi,Yi)表示市场位置,它是已知的.(xj,yj,wj)表示商店位置及其经营规模,W表示总需求量,α、β表示空间相互作用参数,在不考虑供应条件(资源条件时),Williams,金和Martin(1990)提出两个准则来确定最优地域结构.以Z(N)记目标函数,准则1是福利最大准则,即使购买者到商店费用最小.其等价形式结合空间相互作用规律可写作

(6.3.15)

优结构为

这里ui表xi或yi.

另一准则是使企业利润最大化,企业总是力图使自己以垄断形式控制市场,j商店力图使自己的总收益Zj(N)达到最大,即
Zj(N)=Rj-C(wj)
(6.3.19)
式中,Rj为j店总收入,C(wj)是规模为wj的经营费用,N是商店总数,表示商店总数是Zj的隐参数.进一步规定
![]()
C(wj)=sj+kjN
(6.3.20 b)
对(19)式求导可得
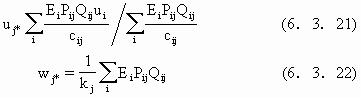
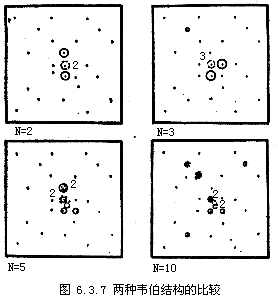
这里Qij=1-pij.图 6.3.7是两种结构的比较.图中实线表示福利结构,虚线表示垄断结构.
在上面的例子中我们看到,韦伯结构并不产生某种特殊的空间图案,这是因为在韦伯问题中市场点和资源点(产业点)是离散的,位置是不确定的.不存在简单的空间划分.韦伯区位问题及其空间结构是近年来引起众多学者兴趣的问题,可以进一步参见新的文献.Drezner,Wesolowsky(1991)讨论了(6.3.14b)中,权系数xi,k是为有负值的情况,这种情况适合于保护某种环境.一般的离数企业与市场的区位问题可以归结为廖什区位问题.
6.3.5 空间网络结构
地理空间的市场与产业分布,不仅是离散的,而且是依赖网络连通的.类似于韦伯结构,考虑市场与产业点均为离散分布,并且这些节点之间由单向流通的弧联结在一起,就引入了空间的网络结构问题.空间网络结构,不仅是产业对市场的配置,而且同时产生弧上的流通,即{![]() ,P,F}.这里
,P,F}.这里![]() 表示市场点集合,P表示产业配置,F表示空间的流结构,也就是涉及的弧及其流量.
表示市场点集合,P表示产业配置,F表示空间的流结构,也就是涉及的弧及其流量.
空间网络结构首先受到需求、供给和流之间货物质量平衡的约束:
![]()
式中,Sk表示k点的生产量或供给量,Sk≥0.Dk为k点的货物需求

是双向连通的,定义为两条弧,这时可能有两条弧总流量受到某种限制的约束.在常见的处理中,认为ua充分大,以至于fka不受最大允许流量的限制.
在空间竞争的条件下,空间结构可能达到了两种状态.第一种是价格平衡结构.第二种是Cournol-Nash垄断结构.对于第一种结构来说,如果流向k点的弧a上的流是正的,则从任意点l运输来的货物价格趋于地方价格k.不然,流为0,即

![]()
上的单位货物运价.(6.3.24 a)表述了价格平衡,它是一种宏观情况,实际上pl+ca≥pk时也可有货物流动.从宏观经济角度来看,长期竞争使pl+ca→pk.
Cournol-Nash垄断平衡结构适应于企业的利益最大化要求.对于企业j来说,它的目标函数是

(6.3.25)
![]()
求量,L为i点全体,vi(Si)为生产达生产达Si量时的i企业成本,fa,i为i的货物在弧a上的流量,这时(23)式改作
![]()
(6.3.26)
![]()
23)-(6.3.26)的计算问题是繁琐的,只能借助计算机求解.
由(6.3.23)-(6.3.26)式确定空间结构,是在市场和企业位置给定下的网络流分配问题.它给定了对于道路网络的空间配置或结构.地理学中还经常处理与产业区位选择联系在一起的网络结构问题,即同时确定企业位置和确定网络的流量,这个问题更为复杂.尚还需学者们探索.Friesz等(1988)讨论了两种竞争的模型及其算法,并且就单一企业的区位选择作了研究.
网络结构问题,还可能更一般化地讨论.设市场容量与企业生产潜力至少有一个量可调的,或者位量可调,流是从企业点i到市场j的道路上进行的.记δ(xi,vj)为从位于xi的点企业流向位于vj的市场的商品流量.在Cournol-Nash准则下我们可能建立一般的空间结构或者区位分析模型.

(6.3.27)


式中xi,vj分别为企业和市场位置,Dj,Si分别为市场j需求和企业i供给,Q为j市场总的营业额,C为从xi到vj调动产品量为Z(xi,vi)的运输及流通费用,F(xi,Si)为位于xi处生产规模为Si的生产成本.适当地选择某些可变量,如Si,xi,Z(xi,vj),固定另外的量如Dj等,我们可能确定空间结构即产业区位、网络上的流量配置.它们的求解,已经引出了大量的文献,在数学运筹学杂志中,不难找到各种具体的变量、J形式(Q,C,F形式)的求解方法和简化模型.可参见Hakimi,Kuo(1991).Current,Storbeck( 1988).
6.3.6 廖什竞争及廖什结构
设空间有若干个企业,资源和市场在空间连续地分布,我们需要考虑的是资源和市场共同与企业(中心)发生作用,这时的空间结构怎样.这里的问题与杜能结构不同,后者仅考虑资源与中心地方的相互作用;它与克里斯泰勒结构不同,后者仅考虑市场和企业中心的相互作用;它类
![]()
我们称对应于这种资源-市场-中心的结构为廖什结构.
廖什结构的形成首先在于中心地方对资源的占据.设区域具有若干个企业(中心).人口的密度为 p(x, y).资源密度为r(x,y),以q(x-x0,y-v0;w)记位于x,y处的居民对位于x0,y0的企业产品的需求函数,参数w表示工资水平.l(x-x0,y-y0;w)为给定工资水平w下x,y处劳动力(资源)对中心(x0,y0)的供给函数.于是我们可以求出中心地方可允许的商品生产量和可能的劳动力(或资源)供应量.
![]()
(6.3.28)
![]()
(6.3.29)
式中,M为总人口数,S为总资源数,Ω0为市场吸引范围,Rs为资源吸引范围,参数w对劳动力资源来说可被理解为工资,也可理解为更一般的资源价格.不失一般性,下面仅就劳动力资源来讨论问题.式中q可能具有相互作用exp(-βr),r=[(x-x0)2+(y-y0)2]1/2的某种形式,也可能取作廖什形式的

(6.3.30)
这里b是市场商品价格.a为生产成本,可能是企业规模与位置的函数,c是单位距离商品单位价,完全类似,劳动力供应l(x,y),也可能只有exp(-βr)的某种形式或者廖什形式,特别可以取作

(6.3.31)
这里s0为某一常数,w0为工人工资均收入,k为单位单劳动力通勤量,显然这是一个极为简单的情况.在上述q,l的函数形式取法下,我们可以取Ω0,Rs均为(-∞,∞)使得积分简化.
由(6.3.28)式求出Q0后,我们可能反过来求中心地方(x0,y0)的劳动力需求量L0,由L0反推劳动力需求范围R0,这是一种企业角度.反过来也可以由潜在的就业量Ls推求必要的生产水平Qs,从而估计需占据的市场范围Ω0.这是一种政府角度.容易发现,给定{Ω0(i)},则产生{R0(i)},空间被市场的{Ω0(i)}和资源的{Rs(i)}划分,形成空间结构{Ω0,R0;w},这里Ω0(i)表第 i个中心地方的市场吸引范围,R0(i)为第i个中心地方资源需要范围.反过来资源供应Rs给定,也就将形成特定的{Ωs,Rs;w}.这里的空间结构{Ω0,R0;w}和{Ωs,Rs;w}是各自独立的,并且依赖于“工资”(资源价格)w0,没有理由认为Ω0(i)与R0(i)将重合,同样Ωs(i)与Rs(i)也将可能是不重合的.
为了由Ω0决定R0,首先需要确定资源或劳动力与产品量的关系.常见的作法是取产出为资源的柯布-道格拉斯函数或线性函数.即
![]()
![]()
式中,K为资本存量,当劳动力供应不足.资本充分时,K/L可保持常数,从而使(6.3.32)式化作(6.3.33)式(线性函数),适合于从Ω0决定R0.求解空间结构{Ω0,R0;w}可以分作三步:先由(6.3.28)式在全平面求出Ω0,再由线性生产函数(6.3.33)式,以QD代Q,求出L,并由L0求出R0,其推求公式是
![]()
(6.3.34)
这一过程只能借用计算机迭代估计或者近似分析.
在实际情况下,企业总是力图使自己的利益达到最大,因此企业的Q0,L0是由它的利润决定而不是由最大允许商品需求范围决定的.因此
![]()
0,我们可以求出最大利润时的(Q*,L*),然后利用类似(28),(29)式关系
![]()
(6.3.35)
![]()
(6.3.36)
求出最优空间结构{Ω*,R*;w},常见的工作是令Q或L为某一给定量,如最大限度占领市场Q0或最大限度吸收劳动力L0,求给定条件
![]()
Kshalhase和Ohta(1990)就一维空间的情况,给出了这方面的一个例子.他们取企业(中心地方)位于x0=0,设

(6.3.37)
F(x;w)=mQ-WL-A
(6.3.38)
式中,m为单位产品市场价格,b0,b1为常数,A为生产所需的固定资本,W为名义工资,w为W/m,相当于实际工资.首先设市场半径为r0,于是有
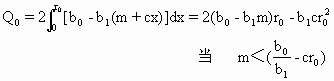
(6.3.39)
或者说
![]()
取Q与 L满足(6.3.33)式,于是将(6.3.40)式代入(6.3.38),并将Q代于γL得
![]()
(6.3.41)
对F关于L求偏导,并令其取值为零得最优条件
![]()
或者
![]()
(6.3.43)
![]()
3.42)式或(6.3.43)式中,我们可以看到,企业可以通过调整工资W或w,或售价m来实现市场控制范围r0的变化,从而竞争市场,或称空间竞争.Nakagome(1987)给出了一组简单空间竞争的解析结果,他发
![]()
问题,正在引起越来越多的重视.新的研究,偏重于从空间动力学的角度展开,这时发现空间结构会出现分叉、突变、混沌等复杂现象.
