3.2 流水过程
3.2.1 泥沙运动
1.泥沙启动

泥沙运移的先决条件是泥沙启动进入水流.泥沙启动的物理图形如图3.2.1所示.设群体泥沙由均匀泥沙组成并且不存在粘结力.水流流经沙粒A附近发生转动.这时产生沿水流方向的推移力FD和垂直水流方向的上举力Fl.记d为泥沙粒径,r为水的比重,ub为作用于沙粒的水流有效瞬时流速,则

式中,CD,C1分别为推移力及上举力系数.a1,a2为垂直于水流方向及沿直方向的沙粒面积系数.这里隐合切应力与u2成正比.再注意沙粒在水中的有效重力为
W=a3(γs-γ)d3
(3.2.3)
式中,γ3为沙粒比重,a3为参数,沙粒起动时FD,Fl的起动力矩应等于W产生的力矩
K1FDd+K2Fld=K3Wd
(3.2.4)
则立刻可得近底启动速度
![]()
实际运用,需要以垂线平均流速U代替近底流速ub.为此取流速u沿垂向的变化规律为
u=ub(y/h)m
(3.2.6)
式中,ub为表层水流流速,h为河深,y为距河底距离,m为指数.在[0,h]间积分(3.2.6)式并除以h则可得平均流速U为
u=ub/(1+m)
(3.2.7)
设y=αd处的流速为作用于沙粒上的平均流速,可得
![]()
代入(3.2.5)可得相应的起动条件下的垂线平均流速,通称启动流速uc
![]()
式中,η为K1,a1等的简化综合系数,沙莫夫于1959年由试验资料建议η=1.14,m=1/6,单位为IS.李保如(1959)认为仅考虑流体与重力的力矩作用是不足的,他认为近壁层流层对沙粒有某种作用,由此他导出η不是常数而是雷诺数Ud/v和相对糙率d/R的函数
![]()
![]()
散粒泥沙的启动流速随水深增加而增加,而且与它的1/2或3/2方成正比.值得注意的是,由于引用(3.2.6)式,所以上述公式仅适合于二维均匀流.在堤岸顶冲、围堰合拢等情况下,只能弓佣(3.2.5)式(谢鉴衡,1981).
如果考虑泥沙细小,互相间有粘结力,并取粘结力N为
![]()
式中,d1为任意选定的参考粘径,ha为与大气压力相应的水柱高度,类似于前面的推导,基于力矩平衡,张瑞瑾导出一个新关系(谢鉴衡等,1981)
![]()
(3.2.12)
式中,C1,C2,s,m为参数。窦国仁建议取C1=1.34,C2=4.96×10-6,s=0.72,m=0.14,d1取为1毫米,d取单位为毫米.
上述理论基本上是基于泥沙大小均匀的假设的.实际上泥沙粒径大小范围是随机分布的.C1,C2等参数的定值可能适合于某一粒径分布的情况.针对泥沙粒径是随机的特点.H.A.Einstein(1942,1950)首创了泥沙运动的统计理论,粒径分布、上举力等都被假设满足某种概率形式,从而引出了一些新的结论.
2.推移质输沙率
推移质输沙率公式有几种估计方法,分别基于动量、拖曳力、能量平衡和统计观点.我们这里介绍的主要是基于动量观点的.
设推移质的运动速度为us,推移质滑动、滚动或跳跃运移的床面层厚度为kd,则单宽推移质输沙率为
qb=γsusmsKdd
(3.2.13)
式中,K为表征层厚度的系数,d为平均粒径约为1-3,ms为动密实系数,它被定义作床面层中运动的泥沙占整个床面体积的比例,也可由过水断面床面层中运动的泥沙面积占整个床面层面积的比例来量度.
泥沙运动速度被认为小于作用于其上的水流流速,有证据支持下列公式成立:
us=A(U-UC)
(3.2.14)
式中,A为比例系数,变化于0.9-1之间.由式(3.2.8),即设流速按指数分布,并且ub与Ubc的关系也为(3.2.14)式则可以导出.
us=A(1+m)am(U-Uc)(d/h)m
(3.2.15)
由实验数据推断动密系数与平均流速U之间有
ms~(U/UC)n
(3.2.16)
成立.将(3.2.15),(3.2.16)式代入(3.2.13)式最后得到
![]()

利用实验数据推断对于均匀沙来说,有
![]()
对于非均匀沙有
![]()
![]()
粒径.如这一组占泥沙统计总体的40-70%,则B为3,如占20-40%或70-80%,B值取25,其他情况下取值15.沙莫夫认为,当平均粒径小于0.2mm,不能运用上述公式计算推移质输沙质.这里导出的输沙
![]()
d和水深h有关,沙莫夫取
![]()
推移质输沙率与d的关系是复杂的.实际上Einstein(1950)认为
![]()
式中,q*是与作用于床面的切应力有关的参数a=(ρs-ρ)/ρ.Swamee等(1991)寻找了q*与河床切应力τ的关系.

而河床表面切应力由下式计算
![]()
式中,γs为泥沙比重,i为河流比降.
Swamee(1991)设床沙粒径的累计概率为
![]()
这里d*是最大粒径,或者说统计中令P=1的最粗组粒径.进而约定

近似地有
![]()
于是

(3.2.27)

这里R是水力半径.不难看出,由统计理论得出的输沙公式是形式复杂的.
3.悬移质的运移
悬移质浮悬在运动水流中运动,悬移质沿垂线的分布决定了它的输沙率.因此对悬移质的垂向分布及由此决定的断面平均单位体积含沙量一挟沙力是推断悬移质输沙率的关键.
关于悬移质沿水面垂向分布有不同的理论.其一是基于扩散方程的.设C是水体的含沙量,由扩散定律
![]()
式中,ω是泥沙流速,εs是泥沙垂向扩散系数.引用二维均匀流条件可得

这里h为河深,ρ为水的密度,τ为河床表面切应力,β为系数,当含沙量为0时,取值为1.再由卡门-勃兰德尔流速公式

式中umax为最大时均流速,u为断面平均流速,κ为卡门系数.对(3.2.32)式求导得
![]()
由于河床表面切应力为τ=rhi,则有
![]()
![]()
![]()
将(3.2.35)式代入(3.2.31)式并化简可得
![]()
取河底边界条件
C(y=a)=Ca
(3.2.37)
求解(3.2.36)式得到

式(3.2.38)中ω/βku*被称作悬浮指标,当ω/βku*≥5,C~0,
![]()
(1925)和Rouse(1937)所建立.
另一种关于悬移质分布的理论是Великанов(1958)建立的.Великанов从能量平衡的观点提出河道含沙水流满足
![]()
式中,U为断面平均流速,a=(ρs-ρ)/ρ.若取相对水深ξ=y/h并取U的表达式为
![]()
δ表示河床相对糙率.在上述条件下(3.2.39)式化作
![]()
取C0为δ处的时均含沙量,有
![]()
实际工作中,由(3.2.42)式可以以数值方法求解C的断面分布.与实测资料相比较,(3.2.38)式求出的C值向上衰减得较快,(3.2.42)式求出的C值向上衰减得较慢.
笔者最近的一项工作力图统一Schmidt-Rouse理论与Великанов理论.取合沙水流是一个热力学系统,在没有化学反应时,我们可有水流系统中的垂向热力学流为:
Jm=-(1-C)Cω(ρs-ρ)
(3.2.43)
![]()
Jm,Jp分为质量流和动量流,对应的热力学力为
Xm=-g
(3.2.45)
![]()
由于达到热力学平衡态时,系统的熵产生σ=JmXm+JpXp应为零,故有
![]()
取ε如扩散理论,则易得
![]()
类似于扩散理论取
![]()
并注意到平原地区i~0,iU>0可得
![]()
![]()
Великанов方程.由此可见,合理的泥沙沿垂线分布,应是扩散理论结果与重力理论结果的某种线性组合.
基于重力理论,Великанов及其后继者导出河流挟沙能力,即泥沙饱和时的断面平均含沙量<C>
![]()
K为某一常数,U为断面平均流速,R为水力半径,ω为沉速.张瑞瑾(见谢鉴衡,1984)等进一步认为
![]()
并且由实测资料推断K≈0.07~0.22kg/m3,m≈1.14~0.76.
考虑悬移质粒径是随机变量,并服从(3.2.24)式,也有类似于(3.2.21)式的公式
![]()
![]()
(3.2.54)
γ1=M0.635
(3.2.55)
δ1=8M(7M1.425+1)
(3.2.56)
3.2.2 河道的基本形态
1.河流横剖面

河道横剖面的稳定形态分析基于两种观点,力学平衡和横向输沙平衡.Lane于1953年基于河床物质受力平衡的观点,提出了一个被广泛接受的模型.他认为底沙受到重力W,拖曳力Fd和上举力Fi的作用,如图3.2.2所示,这时有平衡关系.
W2sin2θ+Fd2=[(Wcosθ-Fi)tgφ]2
(3.2.57)
式中,φ为底沙内摩擦角,θ为河床高部倾角.读者利用初等物理知识即可推出(3.2.57)式.为计算河床横剖面,取Fd=δτ,δ是比例常数,τ是河床切应力,由上分节我们知,它正比于du/dx的平方,Fi一般由两项组成,流水运动产生的上举力和地下水的浮举作用.
Fi=Cfρd2U2+Cugd3(ρs-ρ)
(3.2.58)
式中,d是泥沙粒径,ρs是泥沙密度,ρ是地下水的密度,Cf,Cu是比例系数,将τ的关系与(3.2.58)代入(3.2.57),并注意到cosθ满足(z为垂直水深,y为横向坐标).

将(3.2.59)代入(3.2.57),可以应用数值方法求出河道横剖面.
Einstein(1972)及其后继者从横向输沙平衡角度研究河流稳定的横剖面.经复杂的分析,Ikeda和Izumi(1991)导出河道相对河深ξ满足积分方程

(3.2.60)
式中,S为积分变量.
K1=(ω/ε)hC
(3.2.61)
K2=qBL/qSL
(3.2.62)
r=y/Bγ1/2
(3.2.63)
γ=1850u*hCd/B2
(3.2.64)
式中,ω为泥沙沉速,ε为垂向泥沙扩散系数,B为河宽,hC为最大河深,qBL为侧向推移质输沙率.qSL侧向悬移质输沙率,它们均由河道横向环流引起,y为横向坐标,d为平均泥沙粒径,u*为摩阻流速.显然(3.2.60)-(3.2.64)也能数值求解,然而有意义的是Ikeda和lzumi导出了稳定条件下最大河深(中心河深)与稳定河宽应满足的关系:
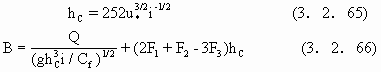
式中,i为河流纵向比降,Q为流量,Cf为河道阻尼系数,一般取Cf=ρghi/u2,u垂向平均流速,F1,F2,F3是与i和d有关的参数.数值分析表明,在上述模型中,河床断面横向断面深径最初的急剧下降后,变成缓慢倾斜,在河流中心达到最大水深hC.
2.河流纵剖面
早在1875年斯恩特贝格就考虑了河流纵剖面问题,他假设颗粒质量的变化dM与搬运距离dx和质量M成正比.于是有
dM=αMdx
(3.2.67)
由于M=αD3(D为泥沙粒径),于是有
D(x)=D(a)exp(-αx)
(3.2.68)
式中,a,α是参数,与具体的地理条件有关,而河床的泥沙大小沿程分布,应与特定的比降保持平衡.在引入这个假定时,一般类比得出河床比降S与河长x有下列关系
S=S(0)exp(-bx)
(3.2.69)
显然这是一种极为粗糙的解说.在3.1节中,我们已经看到,另外的解说将河道纵剖面作为一般的坡面来描述.新近的发展是利用流床过程方程来分析纵剖面形态.这时一般只能求得数值解.例如Bhallamudi等(1992)的工作.而Zhang和Kahawita(1987)则从一维稳定流流床模型,导出最初源区受到一个上升量△G0的干扰后,河床剖面以
S=S(0)exp(-x2/2βt)
(3.2.70)
的形式沿程衰减并趋于稳定值.(3.2.70)式表明,在构造上升干扰后,河床形态向河口地区以x2的指数下降,它比(3.2.69)式来得快.实际上,由于河弯的存在以及沿程河床物质组成的变化,河流或深泓线的纵剖面永远不会是一个简单的函数形式.
3.河流的平面形态
地貌学家和水利学家一般将河道平面形态分作蜿蜒型、顺直型、分汊型和游荡型.其中蜿蜒型和分汊型是基本的.一般的普通地貌学中都包含了大量的关于平面形态的内容.
关于河流蜿蜒的起因,已有大量的学说,诸如最小能耗学说、最大熵学说.但是它们都是不严格的,缺少实证基础.地理学特别重视河流形态的研究,Ferguson(见Gregory,1977)由观察数据提出自然界局部河向偏角满足下列方程
![]()
取θ(s,t)=x(s)y(t),ζ(s)=ξ(s,t)/y(t),(3.2.71)式化作常微方程
![]()
称(3.2.72)式为Ferguson河道方程.进一步地我们取随机干扰ζ为带有随机噪声的干扰
ζ(s)=f(s)+σ(s)W(s,t)
(3.2.73)
这里W(s,t)是零均值随机过程.x代以数学期望<x>后,我们可以化(3.2.72)作
![]()
式中,α,β为参数,分别取值2k(s),K(s)和K2(s)加上f的线性部分.由微分方程定性理论知,当
α2-4β<0
(3.2.75)
时,(3.2.74)式的解是焦点型的.即河向出现波动,河流出现蜿蜒.由此可见河岸“边岸条件”α,β达到一定条件时,河流必然出现蜿蜒.由量纲比较等发现蜿蜒的条件为η1<B/H<η2.这里B为河宽,H为河深,ηi为常数.王铮进一步根据河道演变的规律推断f(s)的性质:当河流处于顺直状态时,河流无非线性干扰,故f(0)=0;其次由于河道的自我调节作用总是力图恢复原有形态或趋向某种平衡,所以f(x)应与x反号,即f(x)是奇函数;再次,由观察事实我们知,|x|较小时,有促进河弯偏角发展的功能.当|x|较大时,河弯阻水,有抑制偏角发展的功能,取临界值为δ,即有
xf(x)![]() 0 当|x|
0 当|x|![]() δ
δ
(3.2.76)
由此,我们设f(x)具有最简单的形式(或取泰劳展开的前三项).
f(x)=βx±εx3
(3.2.77)
当ε=β/δ2>0,是一小量.在这种干扰作用下,应用数学分叉理论,可以发现在一定的宽深比条件下,(3.2.74)式的解将分叉新的解,即同一地点具有两个可能的河向偏角,这就意味着河流分汊.作者的进一步分析发现,沙波在河道分汊中起着重要作用,河流过程在正态随机干扰下输出的河向偏角,其分布不是正态分布,但偏角变化率服从正态分布.其次,用摄动方法求解了(3.2.74)式,得到河向偏角的一个摄动解:
![]()
(3.2.78)
![]()
(3.2.79)
a=a0exp(-αs/2)
(3.2.80)
式中,a0由s=0处的初值条件决定,ε,α是接近0的参数.这个摄动解意味着对于Ferguson河道来说,大约在一个大河曲内部包合一到三个次级河曲.
3.2.3 河床变形与河道演变
1.流床过程基本方程
河道或坡面流床上的含沙水流运动一般被认为是不可压缩的无粘低速浅水运动.大量的研究者研究了流床上含沙水流运动问题.分别发表了一维模型、二维模型和三维模型.一维形式是最简单的,它适于分析河床纵剖面的侵蚀和淤积.Zhang,Kahawita (1987),Bhallamudi等(1992),都用一维模型分析过河道纵剖面演化问题.Bhallamudi等采用河道流床方程如下:
连续性方程
![]()
水的动量方程
![]()
泥沙的连续性方程
![]()
式中,h为水深,q为单宽流量,ξ是河床高程,if是河道水流的摩阻坡(水面坡降),λ为河床物质的孔隙率,qs为河道单宽输沙率.(3.2.82)式的导出考虑了河床物质孔隙率的存在,占体积为1的河床物质仅产生(1-λ)体积的泥沙.为求解(3.2.81)-(3.2.83)式,还需补充结构关系.其一是流量q,qs与水深h的关系.q一般被取作uh,qs理论上讲应由3.2.1中的关系表述,但实际上那些公式过于复杂,因此在近似分析中常用qs与h,u的简单关系来取代.如Bhallamudi
![]()
为均匀流流速.其二,必须确定if与u,h的关系,在这方面有边界层理论或经验公式利用.如Bhallamudi等取i与u,h为谢才-曼宁公式.
一维模型显然不能分析河道在平面上的变形,特别是不能分析最常见的蜿蜒问题.因此发展了二维与三维模型,由一维模型容易写出二维模型
![]()
![]()
(3.2.85)
![]()
(3.2.86)
![]()
(3.2.87)
考虑到qs不显含时间而且h与q的关系大致稳定,上式可以化作较为简单的形式
![]()
(3.2.88)
式中,r为旁侧入流,Dx,Dy为旁侧入流动量的分量,在河道中Dx=0,ix,iy为摩阻坡分量,qsx,qsy分别为纵向单宽输沙(分)率和横向单宽输沙(分)率.与一维模型类似,求解(3.2.84)-(3.2.88)式需要引入关于i,qsx,qsy的经验公式.(3.2.84)-(3.2.88)式的二维模型,在求解河道流床变形问题时存在两个困难,它们主要是由于河流的基本形态是蜿蜒而引出的:首先,弯道使水流的运动更为复杂化,很难认为它是无旋的;其次更为棘手的问题是河道的蜿蜒,实际上定义了复杂的“边岸”条件①,仅考虑河流过程,引出复杂的边界条件.例如在一个正弦曲线上取q,u,v值为零,既难于作数值分析也不可能进行解析分析.因此,在仅考虑河流过程时,最好换用沿主流线方向或深泓线方向定义的曲线坐标(在求解坡面—水道问题时,如3.1.3节所示,引入所谓河道初始化判据).因此发展了基于曲线坐标系的三维和二维模型(Smith and McLean,1984;Shimizu等1992).Smith等取曲线坐标系s,n,z,代替坐标系x,y,z,s表流向,n表横截方向,z表垂向,以R计中心轴线的曲率半径.于是由熟知的坐标变换方法得到流体运动方程为:
![]()
(3.2.89)

(3.2.90)

(3.2.91)
![]()
式中,u,v,w分别为s,n,z方向的流速,p为水头压力,ρ为流体密度,H为水面高程,1/(1-N)为坐标变换系数,N=n/R,当R→∞,
![]()


这里ε如上分节所示为动量扩散系数,由边界层理论取作
![]()
k为van Karman系数(=0.4),h为水深,u*摩阻流速.将(3.2.93)-(3.2.99)代入(3.2.89)-(3.2.92)将引入复杂的非线性方程.对
![]()
中的偏导数项将引出高阶项,从而均可忽视,然而由于s和n方向的二阶项在数值计算时有平滑作中,所以它们的二阶项仍以保留.由此求出三维河道流床方程中的动量方程,(3.2.90),(3.2.91)可化作

(3.2.100)
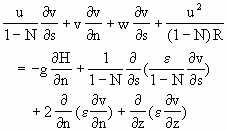
(3.2.101)
在上述方程中H=h+ξ,ξ为河床标高.由此

这组关系将流水过程与河床变形联系起来.与河床变形有关的输沙率关系,在3D模型中分为推移质部分与悬移质部分.推移质是平面运动,故而有
![]()
式中,qb为推移质单宽输沙率.河道中悬移质部分不直接参与造床,它的贡献是与推移质(床沙)发生交换.相应的关于推移质的关系被导出.

(3.2.105)
式中,C为悬移质含沙量,Ds,Dn为泥沙扩散系数相应于3.2.1中的εs,在s、n方向的分解,ωf为动水中的沉速可取作(1-C)ε,qsu为扬沙率,即单位河床面积上推移质与悬移质之间的泥沙交换净速率,Cb为近河床悬移质含量,这两个量必须被参数化.Garcia等(1991),Ikeda等(1989)分别研究了qsu,Cb,发现它们可以视为与流速关系很弱的参数,如Cb=0.0025(u*/(1-C)ω)2.而qsu除了与u*有关外,还与颗粒Reynold(雷诺)数有关.
显然引用上述关系求解河床变形是十分繁琐和复杂的,因此简化模型被引入,首先取河床附近扬沙达到平衡,Cb=qsu/ωρ断面悬移质达到稳定分布,这时(3.2.104)、(3.2.105)可以合并为
![]()
(3.2.106)
Ikada和Nishimura(1987)则建议了所谓的简化的三维模型,S3D模型,他们约定u满足关系
![]()
特别地{}内的项可以作为η=z-ξ/h的泰劳级数展开,这里U为断面平均流速,φ=U/u*,这种处理使得方程(3.2.100)、(3.2.101)的非线性程度降低.另一种近似是以有旋的二维模式(或二维半模式)代替(3.2.89),(3.2.100),(3.2.101)即
![]()

(3.2.109)


(3.2.110)
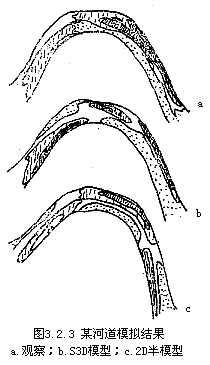
式中尖括号<x>表示对其中的变量x取垂向平均,U,V即<u>,<v>,u=U+u′,v=V+v′.显然这里的关系式中τznb、τzsb等均需要参数化.2D半模型还约定在河岸处,v=0.Shimizu等(1992)用数值方法求解了一个实验弯道的河床变形问题.结果发现,S3D模型与实验观察数据基本一致,2D半模型在弯道入口处没有有效地反映右岸侵蚀,在弯道转向顺直河段处,观察数据和S3D模型都支持左岸侵蚀而2D半模型表现为左岸淤积右岸侵蚀.在弯顶附近,S3D和2D半均以一定的程度与实验数据符合,二者的深泓线方向大致一致(图3.2.3).
实际工作中数值方法求解流床过程,大约有两种方法,一种是首先求解水流方程,如(3.2.87),(3.2.100),(3.2.101),再求解泥沙方程,将ξ的数值代入水流方程,反复迭代.另一种则是直接求解简化模型中全体方程.在解析分析方面,摄动方法被广泛地采用.相比3D模型,1D模型的求解要简单得多,这方面的例子可参见Bhallamudi(1992),Zhang and Kahawita(1987).
2.床形分析
河床不是平直的,其上有沙波运动.由普通河流地貌学我们已知,沙波运动对河道的演化具有重要的作用,它具有促成弯道水流的作用,消耗河道水流能量,引起河道的内部形成各种次生环流,从而促成滩槽变化,同时它本身可以作为边滩来看待,改变水流运动的边界条件.当然,最重要的它是河道输沙的重要形式.沙波覆盖河床形成特有的床形,实验发现床形与水流流态弗劳德数有密切联系,这些内容均可在任何一本现代地貌学的著作中查到.
关于沙波的起因有多种学说,我们不可能全面地介绍它们,本书限于从方法学角度来介绍有关沙波或床形分析的内容.
沙波的形成的一种观点是由于近河床(流床)的流体存在剪切不稳定性.这一流层被认为满足二维欧拉方程

设流层最初是稳定的,u=U0,v=0,p=p0,局部起伏或别的原因产生小扰动使得u=U0+u1,v=v1,p=P0+p1,代入(3.2.111)-(3.2.113)式并注意到U0,P0满足原方程,从而有
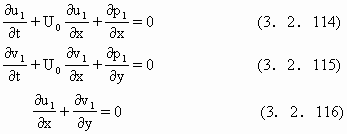
Mahmood,Haque(1988)设(3.2.114)-(3.2.116)具有复数q=Qexp[iα(x-ct)]形式的波动解[这里q=u1v1p1,Q=U(y)V(y)P(y)].代入(3.2.114)-(3.2.116)最后得到
p1=P0e-αycosαx
(3.2.117)
![]()
流速的波动和水压力波动,引起了床而产生沙纹或沙波.而沙纹或沙波一旦产生又作为一种扰动,加强和发展自己.较大的沙波一旦形成,它就作为一种边界条件改变或形成次生环流引起沙波发展.这方面总的来说尚少统一的理论说明.
最近几年中,多相流方法被用于研究流床的运动.在流床上的流体由于包含了泥沙,实际上是二相流,泥沙作为分散相存在于作为连续相的水流或气流中.流床上的二相流的数学形式较为复杂,Ganser和Drew(1990)研究了气床的情况,他们发现原来均匀平直的流床,不需要扰动,只要流体流速达到一定阈值时,流床将发生突变,出现波形,而且波形并不对称.他们分析得出的结论,原则上讲对河床也应是适应的.
3.河道演变的系统分析
流体力学的方法,目前已能较成功地模拟计算河床的变形,但它尚不能有效地分析河道稳定性、突变一类演变问题,因此依据地理学传统,发展了河道演变的系统分析方法.
河道演变的第一种模型是控制论模型.分析者可以适当选取某些地貌特征或水沙特征量如分汊比,输沙率等作为系统的状态特征量,来水来沙状况、河道某些“边岸”条件作为控制变量.例如王铮(1983,1987)对飞云江蜿蜒段建立了控制论模型.作者取(涨潮输沙量—落涨输沙量)/(涨潮输沙量+落潮输沙量)为状态变量x,以上游峃口站流量作为蜿蜒段系统的控制变量,通过系统辨识建立了河道系统方程.由于采用了上述定义的状态变量,平衡输沙x=0被选作平衡点,x在上述定义下是一小量,因此既使系统十分复杂,在x=0附近的小的输沙波动x也可以用线性系统模型近似;换言之,河道系统可能是非线性的,但在某些平衡点附近可以用线性系统模型近似.由实用的系统辨识方法建立的飞云江系统方程是二阶的,利用线性控制理论,作者发现建立的飞云江系统(方程)是完全可控的,平衡点是渐近稳定的,第一个数学结论表示的地貌学意义是,河道的演变受控于上游来水量.飞云江河口,按能量分析属于海相河口,泥沙运行能量来源于海洋动力,其泥沙也来源于长江口南下的沿岸泥沙流,“完全可控”的意义在于上游来水量打破涨落潮建立的平衡(或定向)机制,从而使上游少量的来水控制了河道演化方向,尤如外界信号控制了电视机的输出,但电视机能量却不是来自电视台的.而平衡点是渐近稳定的特点,说明该河段的基本特征,特别是河型是稳定的.
戈韬(1988)及笔者采用类似方法研究了和畅洲汊道的演变问题.他们取(分沙比-1)与(分流比-1)作为输出变量并同时作为状态变量来分析汊道生长问题.以分汊位置和两汊长作为控制变量,采用最小二乘技术辨识河流系统,他们分别建立了1960—1963年的系统模型和1975—1979年的系统模型.应用稳定性判别,结果发现,60年代的系统在平衡点(0,0)附近,系统状态转化阵的两个特征值均在复平面单位圆外,按线性系统理论,这个系统不稳定,必将发生演化.在70年代系统的平衡点(0,0)却是渐近稳定的.换言之,60年代系统由对称型分汊向鹅头型分汊发展,70年代后期则是由鹅头型向对称型发展.
系统分析的另一类模型是自组织模型或称耗散结构、动力系统等.杨志达的最小熵学说等属于这一类.王铮(1989)认为以均匀流形式在河道中流动的水流定义了一维理想河流模型.对于一维理想河流来说,分别建立了它的热力学力与热力学流,由于它们具有非线性关系,按耗散结构学说,理想河道系统具有耗散结构.引用普里高津的超熵生产判据,作者一共得到五个关于河道演变的判据:
判据1 最初处于稳定态的理想河流.如果仅仅含沙量发生小的改变,而比降、水力半径和糙度几乎不发生变化,则无论含沙量如何变化,演变过程是均衡的.换言之,仅仅含沙量发生变化不会发生造床作用.
判据2 最初处于稳定状态的理想河流,它的比降发生小扰动δi时,而糙度、水力半径和含沙量几乎无变化,则河道按下列条件演化.

这里u表示沿河向流速,s为沿河向定义的坐标,g是重力加速度,i是河流比阵.
判据3 最初稳定的理想河流,当它的糙度发生小的扰动δn时,而其它地貌参量的变化又可忽视,河道按下列条件变化.

判据4 最初稳定的理想河流,当水力半径R发生小扰动δR时,而其它地貌学参量不变,河道演化方向仍由(3.2.121)式和(3.2.122)式判断.
判据5 最初稳定的理想河流,当来水来沙项ρ,比降i和边界条件R、n发生小扰动时,则由下列条件决定河流演化趋向:

这里k,k1分别称作地貌扰动指数和比降扰动指数,定义作
![]()
这个判据可以化作能量判据:
![]()
这一关系的物理意义是,水流沿程下降势能V转化为动能K的比值大于k1/k时,河道能量过剩,发生造床过程.
