3.3 海岸过程
3.3.1 动力过程
1.波浪的作用
决定海岸地貌过程的动力过程主要是波浪、潮汐和沿岸流.海岸带波浪和沿带流有密切的联系,它们共同作用运移泥沙,塑造地貌.
波浪的第一个地貌作用是波浪传到沿岸带后,由于水深变浅,底部发出摩擦而发生波浪破碎,第一次波浪以后生成新的振幅、波速的波浪,传到近岸地区将可能发生第二次破碎.习惯上将第一次破碎后波浪称为激浪,第二次破碎后生成的波浪称为溅浪.第一次破波线以内范围称海滨,其外称滨外.
引用2.3.1节中的波浪运动方程,采用特征线分析方法,取切应力τ=0的第一特征位置为第一次破波位置,可以得到
![]()
![]()
浪振幅.在经验公式研究方面,通常给出一个两参数破波判据:
H≥0.020gT2
(3.3.2)
这里H是波高,T是波动周期.实际上波浪是随机的,波浪破碎是随机的,Greenhow(1989)研究了波浪破碎事件发生的概率,其形式是较为繁琐的.破波是随机的,破波的位置也因之是统计的,因此破波带形成的水下地貌沿岸坝与槽的位置也只能有统计意义.
波浪传输到沿岸带后,其主要运动形式可视为孤立波(垂直入射)和边缘波(近于平行海岸传播的).边缘波的形式可取作斯托克斯波.取x方向为沿岸方向,y为正交海岸的方向,斯托克斯波形式为
![]()
(3.3.3)
其中ω取值gksinβ,β为滩面坡度,k为波数,坐标系y垂直海岸,x沿岸,z向上,设波浪平行方向传播.(3.3.3)式的特点是在y=0处波浪振幅达到最大,而且波剖面有净的水面变化.
![]()
(3.3.4)
边缘波作用下,岸线的瞬时位置是沿岸波动的,Yeh(1992)给出,这种情况下岸线位置为-A[cos(kx-ωt)+(1/2)Akcos(2kx-2ωt)],显得复杂化.
波浪的作用在沿岸带起动并运移泥沙,波浪对滩面(流床)的摩擦作用被多数作者认为是正比于滩面上波浪水质点速度u的ub|ub|,即
τ~-Cbub|ub|
(3.3.5)
这里Cb是参数.然而一些作者则倾向于赋与τ与u以更复杂的形式.如
![]()
这里,h为水深,ub也可能以平均流速U代替.当存在沿岸流时,这个关系可能更复杂一些(Chakrabarti,1989).
波浪对流床上泥沙的作用,在考虑到水下沙波时将趋于复杂化.Shum(1992)发展了一个模型,试图研究波浪作用下沙波泥沙的运动.Shum认为沙波流床是具有渗水能力的,因此在沙波附近水流的运动满足达西定律.在归化有关常数的情况下,有方程
![]()
成立,这里p是流床(沙波面)水头压力,显然它是波浪特征的函数.取波
![]()
后得出了沙波上水质点的速度表示式
![]()
![]()
式中,αm,βm(t) 是由水底波浪特征定的参数,h为水深,δ为沙波长L比波浪波长λ.|uf|具有形式2πεk/gT,ε为流床孔隙率,K为UT/L,U为平均流速,T为波动周期.通过上述复杂的形式我们可以看出沙波上泥沙运动具有复杂的形式.在波浪作用下,在x方向和z方向都可能有净的位移,数值分析结果表明净位移有加强沙波存在的趋势.
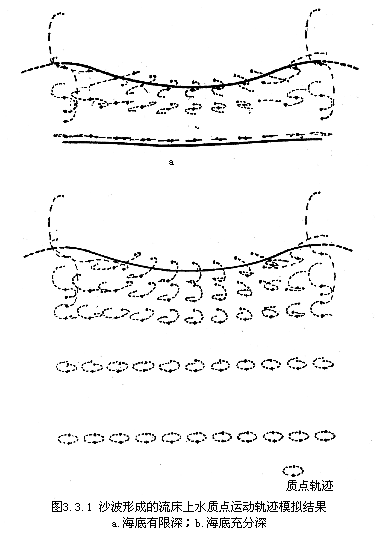
2.滩面上的潮汐动态过程
在滩面上,潮汐带来的潮水发生渗漏,引起滩面过程复杂化.Nielsen①用Darcy定律和连续性方程讨论这一过程

这里ε是孔隙率,K是渗透系数,作者取为常数. 合并上述方程得Boussinesq方程
![]()
滩面上最内侧没有潮汐作用处,定义作x的起点,也就有边界条件
![]()
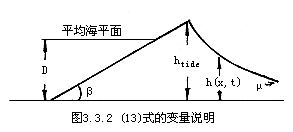
其次在滩面上潮高htide应与滩面倾角有关系(如图3.3.2所示)
h[(htide-D)ctgβ,t]=htide
(3.3.13)
Nielsen求解了三种特殊海岸条件下滩面水深情况:
(1) 垂直滩面和小波动振幅,这时(3.3.13)式相当于
h[(0,t),t]=htide
(3.3.14)
![]()
htide=D+Acosωt
(3.3.15)
求解 Boussinesq方程有
h(x,t)=D+Acos(ωt-kx)e-kx+Bx
(3.3.16)
式中,k为波数,取值[εω/(2KD)]1/2.Bx为常数,对合成波
![]()
有解
![]()
(3.3.17)
这个结果意味着滩面波高随kx增加而衰减.
(2) 垂直海岸-有限振幅:这时仍有(3.3.14)式成立.以D为小参数作摄动处理,得到关于滩面潮波或波动的二阶解
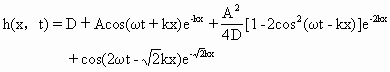
(3.3.18)
(3) 斜坡-有限振幅:利用上述两个方程,作者得到
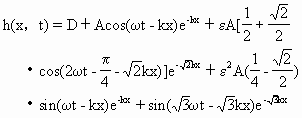
(3.3.19)
利用(3.3.19)式,我们可以由Darcy定律求出滩上的U(x,t),从而推断水流的拖曳力(床面切应力)τ,和对泥沙的起动能力.
3.沿岸流
沿岸流是近岸带主要的和普通存在的流动.在很多海滩上,在沿岸沙坝和槽谷地带,入射波浪发生破碎,并再次形成波浪,近岸处发生第二次破碎,沿岸流及沿岸输沙流活跃在这两个破波线间的激浪带中并且在横向上呈多个强度峰值分布.风的拖曳波浪及近岸环流系统共同产生了沿岸流,并且使它复杂化.传统的理论地貌学对沿岸流的产生较多地归因于波浪在海滩上的折射作用.从动量平衡试图说明沿岸流的特征.关于这方面的说明可见Scheidegger(1970,p.302—303). 他介绍的内容起自于Putnan和Munk等1949年的工作,这是较为粗糙的,其理论的概要大致是:破波线上微分AB范围内的波浪斜向入射海滩,其平行于海岸线万向的动量分量为UCρQsinαcosαdx/λ,这里U是流速,C是波速,Q为AB内侧的水量,ρ是水的密度,α为波峰线(破波线)与岸线交角,dx是AB在岸线上的投影长度.在激浪带如沿岸流的流速为V,则它带走的动量为uVρQcosαdx/λ,一部分动量因水体摩擦滩面而损失,其量为kuρv2ldx,这里k是系数,l是AB 中点取距岸线距离,从而得动量平衡方程
![]()
(3.3.20)
求解这个代数方程得到沿岸流速度的粗略估计
![]()
式中,α取值Qcosα/klλ.显然这个模型是粗糙的,它没有考虑水深的变化,也忽视风力的拖曳作用.因此近年来发展了更为合理的理论,Larson,Kraus(1991)的工作总结了这方面的工作,而最初的理论是由Longuet-Higgins(1962)提出的,称辐射应力理论.这个理论基点如下:沿岸流产生于波浪和风力拖曳,因此沿岸流理论同时考虑两个因素.Mei(1983)提出辐射应力理论作沿岸流分析的几个基本假设:1)沿岸地带具有均匀的波浪、风力和水下地形;2)忽视横截岸方向的底部摩擦;3)波浪是线性波;4)动量、质量平衡.由此他导出在横截方向(x方向)上有平衡关系:
![]()
(3.3.22)
在沿岸方向(y方向)有平衡关系
![]()
(3.3.23)
式中,ρ是水的密度,g为重力加速度,h为静水深,η为水面波浪起伏,V为沿岸流流速,fby,为沿岸流在沿岸方向受到的底摩擦力,Sxx,Sxy分别为x方向和y方向的辐射切应力分量,它的意义是“波浪出现而产生的剩余动量流”(参见Longuet-Higgins1970).取值为
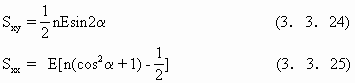
这是E为波能密度,取值ρgH2/8,H为波高,α为入射波浪方向线与x轴的夹角,即波峰线与岸线的夹角,ρa为大气风密度,CD为风力拖曳系数,W为风速,φ为风向与x轴的夹角,n为与入射波浪有关的参量,采用线性波假设
![]()
(3.3.23),(3.3.24)右边第一、第二项分别为波浪和风的作用力,风向定义为指向海洋线为正.ε为粘滞系数,取值与l2umH,这里l2为表示侧向动量传递的经验系数,相当于掺长,um为水底波浪的水平分量,在线性波假设下为
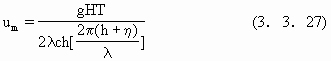
式中,λ为波浪的波长,T为波动周期.ε有两个重要的性质,在水底为充分深时,波高H→0,ε→0.在平坦的滩面上H与h正比于xtgβ,ε~x(gh)1/2,它在激浪带向海方向单调地增加.
在(3.3.23)式中,左边第二项表示沿岸带所受到的摩擦作用,它被从理论上导出应为
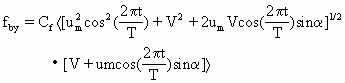
(3.3.28)
这里Cf为摩擦系数,<>表示对波浪周期求均值.因为(3.3.28)形式复杂,实际工作中采用了较简化形式.Bowen(1969)等建议
![]()
(3.3.29)式成立的条件是沿岸流速度明显小于水质点轨迹速度,并且波浪的入射角较小.Kraus和Sasaki(1979)采用了弱流近似但放弃了小入射角假定,给出
![]()
Nishimura(1988)则同时放弃两个假定但引入了波动方程二次近似,这样有
![]()
式中,Z与z分别定义作
![]()
(3.3.32)
Z=2um/π
(3.3.33)
具有式(3.3.23)-(3.3.33)的关系, 可以对沿岸流作数值求解.在实际求解工作中,也可以将fby/V,ε(h+η)参数化为与坐标有关的参数而求解(见Larson和Kruas 1991).在早年Longuet-Higgins则给了一个近似的解
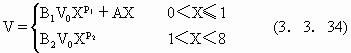
式中,X为相对坐标,等于距岸x与破波位置。xb的比x/xb,v0为与破波水深hB和破波线处入射角有关的参数
![]()
![]()
p约为0.1或取值为与πSN/2a*fw,pi=-3/4+(-1)i+1(9/16+1/p)1/2,S为滩面坡度,N,fw为变数,需要现场估计.
Myrhaug和Slaattelied(1989)不是基于辐射应力理论,而是从线性化的有旋有粘流体力学方程(Navier-Stokes方程)出发,求出了沿岸流垂向分布的一解析解

(3.3.36)
![]()
阻速度,ξ0=k0/δ-1,kb称床沙Nikuradse 糙度,常参数,δ为与水
![]()
水质点波动振幅,ka为与糙度有关的数,
![]()
![]()
沿垂向对沿岸求平均流,最后可以得到沿岸流的平均流速
![]()
(3.3.38)
这个关系与(3.3.36)式比较,平均的沿岸流流速比表层的V值来得小,沿岸流动主要集中于表层,这就可能说明为什么泥沙在沿岸流作用能搬运很远,因为它“漂浮”在表层海水中.
沿岸流流速横向上不均匀,因水的粘滞作用产生出次生的剪切波动.最近的几年,对沿岸流的剪切波及其不稳定性给予了研究,剪切波的作用使得沿岸地貌发育将趋向更为复杂,特别是它的不稳定性的地貌意义,有待进一步认识(Bowen,1989;Dodd &Thornton,1990).它的一些特征,似乎有助于说明水下的某些韵律地形和沙波.
上面的分析中,强调了波浪的作用,实际上沿岸流也可能主要由于风力作用引起.定常的风引起较为稳定的近岸环流系统,近岸环流在内滨区引起沿岸流动,表现为沿岸流.这种成因的沿岸流的分析理论就是近岸环流系统的分析理论.从地貌角度看近岸环流系统,将沿岸泥沙带到滨外,为浅海沉积提供泥沙并形成水下三角洲等,同时环流系统又加强或发展了海岸的韵律地形.近岸环流系统分析的模式,已见第二章第三节.此外,这种环流系统,在破波线附近,冲破阻挡它的水体,形成高速而狭窄的水流,称为裂流,它补偿了两个裂流间的向岸的水质量输送,因而具有重要的意义.限于作者所见,目前尚未看到联系破波作用与裂流作用的分析模型.这样的模型,至少需是三维的,而且不能不考虑复杂的海洋条件和非线性效应.
4.泥沙输运
近海地区泥沙的输运量被认为正比于输送它的波潮流作用力.为了进一步分析输沙关系,一般需从推移质与悬移质角度分别考虑.推移质运动主要起因于水流运动的拖曳作用,因此输沙量qb(t)被认为有下列关系
qb(t)~τ~u|u|
(3.3.39)
这里u为流床附近水质点流速,也可解释垂向平均流速,这相当一个常数.然而有的学者认为上述关系过于简单,Bailard(1982)建议
qb(t)=c1u|u|n+c2|u|mib
(3.3.40)
这里ib为海滩(流床)比降,向海方向为正.实际上比河流输沙更为复杂海水的问题是波浪是复合的周期运动.同一波浪内,可能包括若干个波动频率的波动,因此泥沙运动、输沙也象波浪一样存在一个频谱分布.由(3.3.43)式知u与qb的关系是非线性的,所以当我们确定波浪谱时不能简单地确定输沙谱,从而推知床沙的运动规律,而床沙(推移质)的运动周期对分析港口问题、港道问题时是重要的.Chakrabarti(1989)取泥沙的输运规律满足(3.3.39)式的形式,垂直于水流的柱体对泥沙(包括悬移质)的拖曳力为
![]()
式中,σu为每种周期波动的平均流速u的方差,KD为常数,可以证明
![]()
经过谱变换可以推出拖曳力谱与波浪谱有关系
![]()
这个关系当u叠加上一个定常的沿岸流时,仍然成立.
前面的讨论,一般是针对推移质的,类似于河流过程,对悬移质的分析首先是关于悬移质分布的.Amos和Tee(1989)由扩散定律提出一个关系估计悬移质离岸分布.这个模型被他们称作箱模型
![]()
式中,U是垂向平均流速,C是潮周期内平均含沙量,A(x)是海湾或河口横截面积,μ是水平扩散速度,F是泥沙外源(含床沙扬动悬浮)强度.这里强调潮周期是因为海水中悬移质细而均匀,波浪的作用由对流体质量的输送效应引起,在一个波动周期中,线性波的净输运为零.结合潮波运动关系,如2.3.1节所介绍的或关于U的经验公式,可以求出C的变化.这里的工作方法,类似于河流中流床问题的计算.值得注意的是(3.3.44)式的U如果与潮流计算对应取为矢量(u,v),对非海湾悬移质分布,可以将A取作单宽A=1来计算,这时隐含海岸是无纵向变化的假设,在这种情况下,Amos等还给出了一个泥沙离岸分布的统计估计
C(x,t)=C0(t)exp[-K(t)(y-y0)]
(3.3.45)
这里C0(t)是y=y0处的悬沙含量,K(t),C0(t)由经验估计.
如果考虑波浪运动的非线性效应,已经知道在一个波动周期,有限水深的波浪,净质量输送不为零.例如我们前面知道的孤立波的净质量输送.对于艾里波来说,净质量输送速度U为
![]()
这里的符号意义同2.3.1,C为波速,可以认为悬沙输送率与其成正比.
Bailard(1981)引入了一个计算推移质和悬移质输沙总量的关系,适合于描述横向输沙
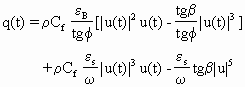
(3.3.47)
式中,q是横向输沙总量,ρ是水的密度,Cf是拖曳系数,φ是内摩擦角,ω是沉速,εB,εs,分别是推移质和悬移质的修正系数,β是难面倾角,u(t)由波浪计算估计.
原则上讲,沿岸流输沙率也可类似计算,由理论分析或数值方法求沿岸流强度u,我们可以利用(3.3.39)式估计输沙率.q与u|u|之间的关系系数可以回归估计,以同时反映推移质和悬移质的运动.经验上认为沿岸输沙率是沿岸流功率Pl的函数,故而也可由沿岸流计算Pl进而
![]()
Pl=(ECn)bsinαbcosαb
(3.3.48)
式中,(ECn)b为破波带的波能通量,αb为破波波峰线与岸线夹角,(ECn)bsinα表示了沿岸方向的分量,再乘以cosαb是因为海岸线单位长度上获得的波能通量是(ECn)cosαb,这样看来,sinαb与cosαb同时引入可能是互相矛盾或重复的.另外,Eaton和Longuet-Higgins(据柯马尔,1985),王尚毅(1991)将沿岸流处理为类似河流水流的运动水体,从而导出了q的一个关系, 其形式远较(3.3.48)式复杂,也比一般的河流输沙公式复杂,这一例子说明估算海岸带的输沙问题是比河流问题困难的.
在(3.3.48)中ECn表示了波能通量,它表示单位宽度上单位时间内通过的能量.因此它是一个波长内储存的能量与波的传递速度C的乘积.已经证得对于艾里波来说,其一个波长的动能与势能均为ρgH2λ/16,这里H=2A为波高,ρ为水的密度,λ为波长,g为重力加速度,因此平均波浪的能量密度为ρgA2/8.在深水的情况下,总能量一般是按波速传播的(动能不传播).在有限水深的条件下,能量的传递部分需要乘上一个修正因子,1+2kh/sh(2kω),从而有破波以后的能量输送率为
![]()
以E记深水总能量密度ρgH2/8,n记[1+2kh/sh(2kh)]/2,并记Cn=Cn,则波能通量CEn为ECn.有限水深区同时有净质量输送如(3.3.46),也应增加沿岸流强度,(3.3.49)未能考虑.在(3.3.48)式中Cn表示了不同水深环境的波能传播速度,在深水区,n约为1/2,这意味着
![]()
速与波能传播速度趋于一致.
在柯马尔(1985)的著作中,大量地讨论了横向和纵向输沙问题,可以进一步参考.
3.3.2 海岸演化
1.岸滩剖面演化
岸滩剖面变化主要由横向输沙引起.通过水动力过程和泥沙运动规律,我们可能由模拟计算来较精确地分析这种过程、数值模型的基本关系,已为3.3.1节所介绍,这里讨论的是一些较简单的方法,而且主要是针对沙质海滩的.
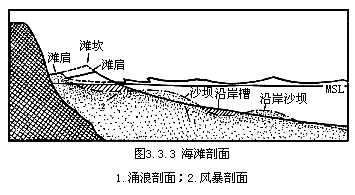
已经发现,海滩剖面有季节性变化.在加里福尼亚海岸的观察,发现季节变化呈冬季型的风暴剖面和夏季型的涌浪剖面.图3.3.1给出了两种剖面的形态特征.从更长的时间角度看,从岸滩及海滩剖面的地貌结构和演化特征方面,可以将岸滩或海岸分作侵蚀型、堆积型和过渡型,后者也可称为平衡型,海岸海滩达到了与水动力条件相适应的稳定状态.为判断剖面类型和海岸性质常引入若干判别标准,它们给定为某些地貌特征(如坡降)和水动力特征(如波高)的组合形式.岸滩冲淤判别关系及阈值如表3.3.4所示(本书图表统一编号).在这些判别关系中,变量H为波高,λ为波长,H/λ称波陡,它表示了波浪的能量特征,由(3.3.49)式可知能量密度与波陡有关,波陡越大,单位波长内集中的能量越多,有利于泥沙向岸运动.当波陡达到一定阈值时,波浪必将发生破碎,破浪结果具有搅动泥沙,形式激浪带和沿岸流的重要效果.i值表海滩坡度,它对海滩冲淤性质的影响是容易理解的.d50(泥沙中径)与λ0的比,实际上是用于反映海滩抗冲性的量,对于给定的波长和波陡来说,d50越大,表明了相动运动越困难,因此需要更大的波能下能引


内,传递的能量或对泥沙的力的作用测度.关于横剖面模拟计算的实例可参见Roelvink和Stive(1989).
表3.3.4中的判别式的建立,基本是假设一种均匀的地貌条件,然后由联系泥沙运动关系和波浪能量、速度关系来导出泥沙运动的平衡条件,再由平衡条件推断冲淤倾向.徐啸(1988)导出了一个海滩冲淤类型判别关系,可作为一个例子来认识.
设滩面以坡度β倾斜,沿坡面方向,沉积物所受的下滑力F和坡面阻力R分别为
F=(ρs-ρ)gVbsinβ
(3.3.50)
R=fw(ρs-ρ)gVbcosβ
(3.3.51)
式中,ρs为沉积物密度,ρ为水的密度,Vb为沉积物体积,fw为浮动条件下的摩擦系数.设床沙输运速度为ub,则泥沙向岸运动时波沙得到的能量应与阻力功相平衡.单位时间内泥沙的阻力功与有效能量eE之间应有关系
(ρs-ρ)gVbub(fwcosβ+sinβ)=eE
(3.3.52)
式中,e为激波带波能有效系数,E为一个波长内波浪的能量,取重量输沙率qb为ρsgVbub,容易得到
![]()
类似地可得离岸方向悬移质重量输沙率为
![]()
式中,es为波能悬沙效率,(1-eb)表示耗去床沙耗散后的剩余能量,us为悬移质运动速度.不考虑推移质离岸运动,并取e=es(1-eb)/eb,可得
![]()
![]()
为破波点或深水区特征量,从而可有


(3.3.56)
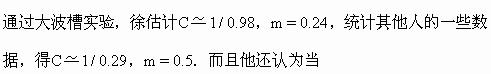
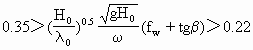
(3.3.57)
时,滩面处于相对平衡状态.
与区域的波潮流条件适应,滩面可能趋向于“平衡剖面”,(3.3.57)式实际上是平衡剖面赖于存在的条件.平衡剖面的平衡是动态的,水流上冲返冲产生的动力与滩面上重力产生的下滑力达到平衡.由(3.2.1)知水流作用于泥沙的牵引力为
![]()
式中,CD为拖曳系数,d为泥沙粒径,ρ为水的密度,ub为床面附近流速,a为某一参数.水中的下滑力相应地为(ρs-ρ)gsinβ,这里ρs为泥沙密度.在达到动态平衡时,应有
![]()
上述关系中,a应进一步理解为上冲与返冲达到的某种平衡的净上冲效
![]()
CD~1/Re,上述关系可以化作
sinβ=Cd<ub>
(3.3.60 )
C为新的比例系数.(3.3.60)式指出,海滩面物质粒度越粗,滩面的角度越大.由于ub可能与β有关,不能认为δ与sinβ简单地成正比.如取滩面上的波浪为有限深度的斯托克斯波,有
![]()
<h>为平均水深,它与滩长L可有关系<h>~Lsinβ,注意到β~0,故有
sinβsh22πkLβ~k2H2d
(3.3.62)
平衡滩面倾角与波数k,波高H和粒径d均有关系.
当区域的波潮流条件发生变化时,原来的平衡剖面必然会被破坏,特别当海平面上升时,这种变化是系统的.滩面的演化,被认为服从(3.1.1)式所描写的坡面方程
![]()
Scheidegger认为,侵蚀函数φ在海岸的情况下取为asinβexp[-α(Y-y)2]的形式.这里Y是水面距某一基面的距离,a、α为常数.注意到
![]()
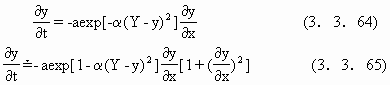
这一方程在给定Y(t)的形式下,如海平面上升Y=Y0+f(t),可以数值求解.我们认为Scheidegzer取φ为Y-y的二次指数型不尽合理.在φ的关系中,sinβ考虑了坡面作用,exp[-α(Y-y)2]考虑岸滩上水流拖曳力的衰减,由于τ~u|u|,由3.3.1第一段的讨论,在滩面上u~exp[-α(Y-y)](这样Y取任意值时,均可保证只相差一个常数).故而,φ似应取为(Y-y)的一次指数形式.在(3.3.64)式成立时,取f(t)为f0t,即海平面线性上升,Scheidegger得到岸滩水平后退速度大致满足:

的形式,即后退速度R为一个常数.
2.岸线轮廓演化
岸线演化的模型是建立了沿岸输沙基础上的.在本段中我们用x表沿岸方向,即纵向,y表垂直海岸方向,即横向,这种表示与前面几节正好相反,请予注意.这种表示主要是为了顺应数学上的习惯.设长度为△x的一段岸段,设Si为泥沙输入段的速率,S0为泥沙输出段的速率,在△t后,该段净的堆积与侵蚀量为△V
△V=(Si-S0)△t
(3.3.67)
显然,若△S=Si-S0>0,该岸段堆积,若△S<0,该岸段侵蚀.另一方面当岸滩的高度为h时,侵蚀的体积或堆积的体积为△V=h△y△x,由此可得泥沙沿岸运动的连续性方程
![]()
这一方程可以与沿岸流输沙公式,如
S=r(ECn)bsinαbcosαb
(3.3.69)
联合求解,对于一阶偏微分方程(3.3.68)来说,代入(3.3.69)后只能由数值方法求解.Peluard-Cousidere认为S的变化只是由于破浪角αb引起的,将S展开为αb的泰劳级数
![]()
借助方程(3.3.70),他们求解了顺直岸线在垂向建筑了丁坝或突堤后的岸线轮廓,其形式较为复杂.王铮(1985)从泥沙扩散角度提出岸线演化大致满足
![]()
![]()
的扩散方程.作者针对几种情况分析了岸线的演化:
第一种情况为三角形海湾,这种情况下(3.3.71)式的定解条件为
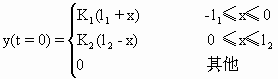
(3.3.72)
由初值条件式,按扩散方程的形式解得到岸线演化为
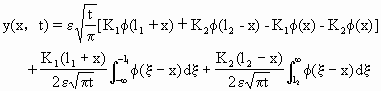
(3.3.73)
这里φ(x)=exp(-x2/4ε2t).对地貌学来说,有意义的是岸线冲淤速度,对一般初始岸线φ(x)来说,
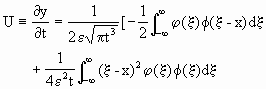
(3.3.74)
![]()
到的,于是由积分第一中值定理可得
![]()
式中,θ为反映岸线对称情况的参数,θ=0, 岸线关于湾顶对称.(3.3.75)式给出不冲不淤点的位置为
![]()
它是两侧的,与岸线不对称参数θ有关.(3.3.76)式指出,冲淤平衡点是移动的,随时间演化,靠近湾顶的岸段越来越多地趋向淤积.
第二种情况为曲线岸段,这时定解条件化为
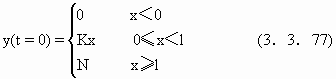
岸线演化
![]()
![]()
作者进一步证明,这时的冲淤平衡点位于x=l/2处,岸线演化发生凹角填充,凸岸侵蚀后退.
作者建议河口由于其河宽与海岸线相比趋于零,河长充分长,形式复杂,河流总面积有限,从而有定解条件
y(t=0)=Aδ(x)
(3.3.79)
即河口原始形态是函数.由(3.3.71),(3.3.79) 式得到河口基本形态是高斯误差函数
![]()
王铮利用飞云江的岸线资料证明了(3.3.80)式描述的河口形态是正确
![]()
海线淤长,在外侧,海岸冲刷.由于沿岸流的作用,飞云江口外岸线呈总的冲淤趋势,但岸线形态还是服从(3.3.80)式的形式,多年岸线演
![]()
变化点.所谓“平行”推移,是将岸线按正态对数坐标变换后,标在正态坐标纸上,两侧岸线,各自平行.“平推”过程中,河口地区河道的“海湾”性质消退,河流性质增加.
