3.4 其他地貌过程
3.4.1 冰川过程
1.冰川的滑动
冰川滑动的模型一般是基于固体力学的,或者基于流变学,后者有更复杂的形式.比较流行的是Nye于1952,1955建立在塑性理论上的模型:
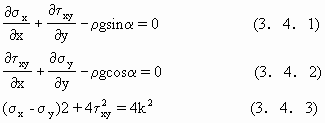
(3.4.1),(3.4.2) 式是力学平衡条件,表征单位体积冰受力情况,(3.4.3)是塑性屈服条件.式中,σx,σy为正压力,τxy为切应力,k为屈服函数,与材料有关,α为冰床坡度,ρ为冰的密度,y轴定义垂直坡面向上,由冰床上τxy=k知冰川厚度满足h=k/(ρgsinα),考虑在冰川自由表面y=h处,σy=σx=0记h0=k/ρg,可以得到

再由连续性条件
![]()
和应力主轴条件
![]()
可以得到冰川运动速度
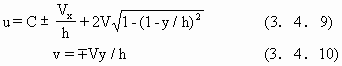
式中,C,V为常数.第一个解具有冰川物质“向上挤”的特征,第二个解则“向下挤”,从而得到两组不同的塑性体滑动线.上述分析中取冰川表面为自由表面,因此,当有雪覆盖时应一同计算.
上述模型考虑冰床是平坦的,后期的一些工作考虑了冰床上有障碍物的情况和冰川运动过程中应力作用而引起冰溶的情形.Lliboutay 1967年建议以正弦波动描述冰床
![]()
式中,z是冰床高度.定义凸凹度(rogosity)为
r=a/λ
(3.4.12)
由于冰床凸凹不平,这样冰床上的正应力σz也会变化,并设为
![]()
这一关系设床面最高处,σz=ρgh.在一个波长范围内,平均的摩擦拖曳力F为
![]()
另一方面最小床面正应力为
σzmin=ρgh-△σ/2=0
(3.4.15)
后一个等号考虑当冰与床分离时,应力化为零,故有Δσ=2ρgh,代入(3.4.14)式得
![]()
实际上如果发生冰床分离,则融水充满其间,所以(3.4.14)还应加上0℃,水汽平衡压力,故拖曳力应为
![]()
![]()
过较繁琐的分析,作者得到实际的拖曳力为
FC=π2rδ(gρh-ρ)/λ
(3.4.18)
这个关系可以物理理解如下:虽然冰川以F为冰面切应力,在床、水分离部分,切应力只作用在融水上,水不传递切应力,只有在不分离的2δ范围内,F才有造床作用,故切应力F应乘上弧度因子2πδ/λ才是真正的拖曳力.关于因子π2,应作为与床面形态有关的比例因子来处理.
2.冰川动态
冰川覆盖于地面并呈近于固态的形式,所以它的动态具有直接的地貌学意义.冰盖形态的一个经典模型是Orowan(1951,见Scheidegger,1970,pp.370—371)的,它是关于冰帽的、设冰盖由于重力作用向前延伸,冰床粗糙,其上作用有切应力τ=K(即上节Nye模型),这样dx乘以单位宽度的冰体所受的力为
F=Kdx
(3.4.19)
同时从底部到表面平均的正压力为1/2ρgh,h为冰盖高度.由于h是x的函数,可以导出,单位宽度冰所受的x方向力R
![]()
近似有
![]()
两个力应平衡,得
Kdx=ρghdh
(3.4.22)
结果得
![]()
取L为冰盖长度,则有解
![]()
式中,h0=K/ρg,这个解意味着冰盖(帽)形状为抛物线形.
冰川前鼻形状及其形态是最为引人注目的.设冰川运动速度为(Scheidegger,1970)
V=Khn
(3.4.25)
溶化速度为a,则实际前鼻进展速度为U=V-a, 因而连续性方程为
![]()
它可化作
![]()
这里n约为1/4-1/2,K与冰床坡降有关.这个方程可由数值方法求解,它描述了前鼻形态.
一般的冰盖动态满足连续性方程(Mahaffy,1976)
![]()
![]()
是降水凝结加积与消融量之代数和,us由力学计算估计,如(3.4.9)和(3.4.10)所估计.消融量还可以通过气象学关系来估计,从而得到冰盖动态的分析模式.在气侯演变分析和冰川运动研究中,上述模型可被用于数值分析,新近Macayeal(1992)建议了一个考虑粘滞性的冰川运动二维方程.加积和消蠕的一些实用模型已经被建立了.消融的模型与大气过程有关,加积与消融过程决定于冰面温度和其毗邻的冰水温度,后者又与气温可能达到某种平衡.Karoda(1985)建议了一个海冰生长的微分方程,近似地可以用它描述一般的加积
![]()
式中,L是溶解潜热,ρ是密度.C是热传导系数,Tm是冰水温度,Ts是冰顶面温度.用
![]()
代入(3.4.28)或(3.4.27)式, 我们可以求出有冰生长的冰川形态动态.求解(3.4.30)式,并取t=0时h=0,有解
![]()
这就是说在水分供应充分时,冰的生长与t的平方根成正比.当地下水饱和时,这个结论也可以用于冻土中地下冰的生成分析.
3.4.2 冻土过程
1.冻结过程
土层的冻结过程根据是传热学理论.如考虑土是均匀的,水的蒸发耗热量可忽视,热传导、质量传输为液相迁移以及冰水相变,忽视对流作用,则冻结过程满足
![]()
如果进一步考虑冰的生长,则有
![]()
式中,C是热容量,λ是热传导矢量,ρi是冰的密度,ρu是未冻结水的密度,L是潜热,Vi是冰的体积,这个方程需配合下式求解
![]()
φ是地下水压力水头,K是弥散系数,它描述冰体积生长.
实际上由于计算复杂,K又难于确定一般不用(34)式,而采用参数化方法
![]()
将(3.4.33)式化作
![]()
求解,一般只能借助数值解法(安维东等,1987).
在地温T(摄氏度)与季节冻土或永久冻土的未凝水之间存在下列关系
θ=(ρb/ρu)a|T|b
(3.4.37)
式中,θ为未凝水范围(体积),b为常数,由经验定,ρb是冻土的干密度.
对于冻结过程,Osterkanp 1987年考虑了分层处理的方法,对一维问题作了解析求解,这结果发现在上下层温度分别为Ti-1,Ti时,T(x,t)有
![]()
(3.4.38)
式中,D=λ/C1i;δi为常数,当i=n,δi=0,erfc(x)是误差函数.(3.4.38)式表明自上而下温度升高,随t变大,层的中部温度突变越明显.
2.冻胀作用
土层冻结后,由于同重量冰的体积大于同温度的水,所以发生冻胀作用.反映土冻胀强弱的指标采用冻胀率η.也称冻胀强度,即单位冻结深度增量引起的冻胀百分数,朱强等提出冻胀强度满足下列公式
η=A(WB-W0)+Ba/Vf
(3.4.39)
式中,A,B为常数,他们推荐0.09和1.09,WB为土层冻前含水量,W0为土层中未冻水含水量,a为水分迁移率,Vf为冻结速度,由实验数据他们得出经验关系:

式中,z为该冻土层中心至地下水的距离,单位是厘米.作者认为存在多层冻土层,冻土层上部有一与高冻胀率对应的高含水层,它的水分比冻结前显著增加,而在冻结层下面,形成脱水区.关于这种现象,尚未见模型说明.朱强等认为冻胀深度分布存在多种模式,主要是Ⅰ型和Ⅱ型.分别对应于高冻结层分布在上部50%的冻深范围内,和高冻结层分布在下部50%冻深范围内.
在地面加载的情况下,超载对土冻胀有抑制作用,陈肖柏1983年认为η与有效超载应力P存在下列关系
η=η0exp(-bP)
(3.4.40)
式中,η0是P=0时的冻胀率.b与土层性质有关.有的工作发现,冻胀率与土壤含水量有关,但关于这种关系目前还不明确,多数人采用经验公式.此外冻结速度与冻胀率也有关系.实际上(3.4.39)式反映了η与Vf之间的反变关系.邱国庆等则认为η为Vf的关系是负指数的.
在普通地貌学中我们已经知道,冻胀产生丰富的地貌现象,冻胀的力学效果,一般可引用连续介质力学理论来分析.冻土区还普遍存在蠕动、蠕变、热融喀斯特现象,并形成石环、构造土等重要现象,限于篇幅本书不予讨论.
3.4.3 风沙过程
1.风蚀和风沙输移
风沙运动主要是近地表的.近地表的边界层内风速一般遵循冯·卡门-普朗特的速度分布律.平均流速u为
![]()
式中,η为卡门系数,u*为摩阻流速,y1为u=0对应的y值,约为沙粒凸起高度的1/30.
在风沙流床沙粒起动的流速与流水作用类似.Bagnold提出泥沙启动流速为
![]()
式中,ρs,是沙粒密度,ρ为空气密度,d为泥沙直径,η,A为常数,与泥沙粒径及其分布有关.Bagnold取η为5.75,A为0.1.
风沙的运移与河流泥沙运移有很大的不同.后者悬移部分占很大比重,风沙流主要以推移和跃移的形式运行的.若干风洞实验和野外观察证实输沙率qs与风速的关系u3
qs~u3
(3.4.43)
由(3.4.41)式可知,输沙率与表面切应力τ0有下列关系
![]()
然而有些作者发现,在土壤表面土壤物质的重量W与摩阻流速u成5次方,即与τ0成5/2次方.
2.地貌效应
风沙地貌的主要形态是沙丘.沙丘的最初形成在机制上被认为与河流中的沙波一致.关于沙坡包括沙纹的起因学说较多,这说明对这个问题还很不清楚.一种学说认为沙波是由于流体波动造成的.另外人认为沙波是由于流体与流床组成不均匀造成的.在3.2节中,我们结合蜿蜒问题,介绍了两种河道沙波生成的理论模型.这种模型原则上可以推广到沙波的形成.
地貌上观察,运动沙波在河道中主要是带状、波浪状,在沙漠中主要是新月形沙丘.Scheidegger(1970)建议活动风沙沙丘的速度C为
C=qs/ρbsh
(3.4.45)
式中,qs为单宽输沙率,ρbs是床沙密度,h是沙丘高度.
在3.2节中我们讨论了流床的一些动态规律,可以借鉴到风沙地貌中.值得注意的是沙床上的流体、气流是可压缩的.因此,关于河道流流床的模型不能直接用于计算风沙地貌的流床,必须考虑流体的压缩作用.
3.4.4 喀斯特过程
1.喀斯特发育
碳酸岩区普遍存在的喀斯特地貌主要是由物理化学过程完成的.其反应系列为
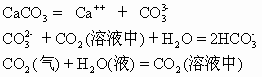
在地下水中,溶液的运动遵循有对流项的扩散方程,记溶液浓度为C,则有
![]()
式中,D为扩散系数,值为2×10-5平方厘米/秒,v是水流流速.由上述过程的化学反应动力学方程可以定量研究洞穴发育.
喀斯特的发育需要借助断裂带,流水首先渗入断裂.Wey1关于稳定流情况求解(3.4.45)①,考虑断裂宽度为d,平均流速为V,V平行于断裂面.结果发现流体的饱和度达90%的体积的距壁距离L满足

当V=1厘米/秒,d=1毫米,有L=1.52米.
Wey1的理论仅仅适合于允许流态为层流的发育完好的断裂带.此外,洞穴或管道的稳定性,显然可以化为固体力学问题.一般仅需借助弹性力学结果或分析.
2.喀斯特演化的模型
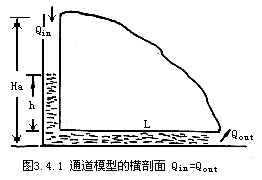
Smart(1988)发展了一个模型可以用说明喀斯特演化的某些方面.这个模型设地下水是管道联系的.如图3.4.1所示的变量系统.由Darcy-Weishach方程
![]()
这里Q是系统流量.r是管道半径,f是Darcy-Weishach摩擦因子,L
![]()
分布
![]()
将(48)化作为关于h0.5的概率密度函数
P(h0.5≥H0.5)=dr2.5exp(-λdr2.5H0.5)
(3.4.49)
![]()
![]()
由Palmer的工作
![]()
式中,K是常数,△C是欠饱和度(Suturation deficit).取t=0,r=a.则
r(t)=K(△C)t+a
(3.4.51)
这样
p(OF)=d[K(△C)2t+a]2.5exp[-λd(K△C2t+a)2.5H0.5]
(3.4.52)
这一关系表明:当喀斯特开始发育时,地下水埋深分布较广;当t充分大时,这个分布也较广;在发育的中间阶段,允许埋深Ha的分布范围较小,这时地下水面接近一致.
