用最小需要量法分析美国城市的经济基础,同样证实了城市的非基本部分随着城市规模的增大而提高(表6-3)。
厄尔曼和达西按城市规模组来确定城市经济的基本/非基本部分,又向前跨出了一步,但仍不是尽善尽美。批评主要集中在两个方面。
首先,假如被选择出来作为衡量某一规模组最小需要量的那个城市,经济结构恰恰很特殊,不能代表一般状况,那就会影响一大片城市的计算的准确性。厄尔曼和达西的研究只把美国城市分成6个规模组,规模间也不连续,每个规模组只随机选择38个城市(100万以上级别为24个样本)。由于种种原因,的确使某些所选城市的代表性受到了怀疑。例如,首都华盛顿特别低的耐用品制造业和批发业比重被选作100万以上城市的最小需要量指标就是最突出的例子(表6-3)。
表6-3 美国14个部门不同规模组城市的最小需要量(%)
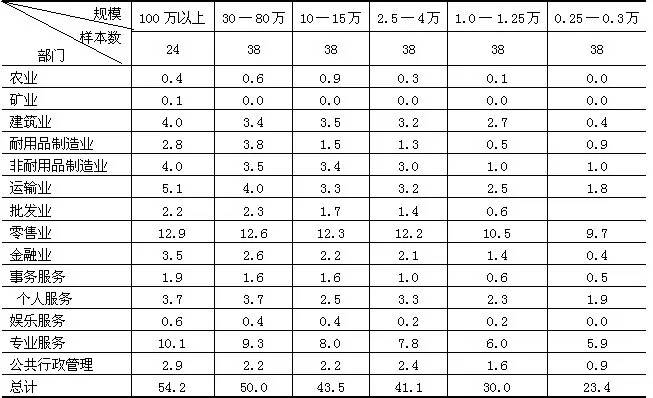
另一更尖锐的批评认为,假如按照厄尔曼等的方法认为具有最小需要量比例的城市能满足自身需要,其余城市都有输出,那么就会得出一个矛盾的结论:几乎所有的城市都有输出,却没有一个城市需要输入。这一点也许正是最小需要量法与区位商法、正常城市法相比,在理论上的一个漏洞。批评者半开玩笑地说:不是所有高于最小需要量的城市输出货物或服务,而是所有高于最大需要量的城市输出货物和服务。
以上两个缺点已经被另一些研究者设法克服,使最小需要量法日益趋于完善。
为了避免第一个缺陷,穆尔(C.L.Moore)把城市按规模分成连续的14个等级,从每一个规模级的城市样本中,找出每个部门的最小职工比重和中位城市的规模。然后将两者进行回归分析,利用回归方程可以求到任何规模城市某部门相应的最小需要量。数学表达式如下:
是i部门P规模城市的最小需要量,
和
是参数,,
用下式求得:
是第j规模级别城市中第i部门实际找到的最小职工比重,
是第j规模级城市的人口中位数。
穆尔对1970年美国333个城市的分析结果表明(表6-4
) ,大多数部门的城市规模级别与最小需要量之间有很高的正相关。出乎意料的是零售业相关性不强。建筑业、健康服务业和农业则没有相关性,故没有包括在图表中。所有部门都表现出最小需要量随城市人口增加而上升的趋势,其中以耐用品制造业最显著。
表6-4 穆尔回归分析的相关指数()
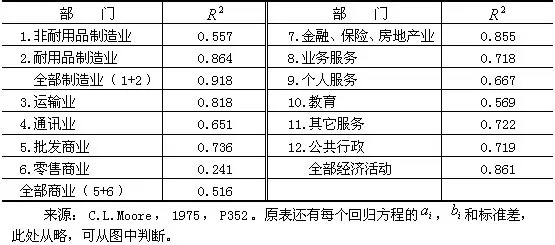
为了克服厄尔曼等方法中的理论缺陷,吉布森(L.J.Gibson)和沃登(M.A.Worden)改用各规模组中第二位最低的城市职工比重作为每个规模组城市的最小需要量。他们为了从各种方法中找出最佳区分基本/非基本的间接方法,曾经对亚利桑那州的20个小城镇(人口从1838到15 000)用普查法、三种不同比例的抽样调查法、两种不同标准的区位商法和四种不同的最小需要量法进行对比研究。结果证明,用穆尔建立的最小需要量的回归模型所得的结果最接近于普查结果。用第二位最低职工比重的最低需要量法效果也相当好。
三、影响基本/非基本比率的因素
城市B/N在不同城市之间有很大差异。
首先是随着城市人口规模的增大,非基本部分的比例有相对增加的趋势。城市越大,城市内部各种经济活动之间的依存关系越密切,城市内的交换量越多;城市居民对各种消费和服务的要求也越高;城市也越有可能建立较为齐全的为生产和生活服务的各种行业和设施。而小城市一般只有很小一部分的生产和服务是维持本身需要的,基本活动部分比重较高。
在规模相似的城市, B/N也会有差异。专业化程度高的城市 B/N大,而地方性的中心一般B/N小。差不多规模的城市,如果一个是位于大城市附近的中小城镇或卫星城,另一个是远离大城市的独立城市,则前者因依附于母城,可以从母城取得本身需要的大量服务,非基本部分就可能较小;而后者必须建立自己较完整的服务系统,非基本部分就较大。
老城市在长期的发展历史中,已经完善和健全了城市生产和生活的体系,B/N可能较小,而新城市则可能还来不及完善内部的服务系统,B/N可能较大。
城市经济的基本/非基本部分的结构随着时间的推移也有变化,厄尔曼等对美国14个部门1940、1950、1960三个年份的城市最小需要量比重的分析发现,有些部门的最小需要量随时间变化相当稳定,而个人服务和专业服务两个部门的变化幅度相当大。可能因为家庭仆役人数的减少,前者的最小需要量1940年以来大大下降;可能由于咨询业的发展,后者的最小需要量大大上升。穆尔的分析也表明,1940—1970年期间城市总的最小需要量比重,总的说呈不断上升的趋势,在大城市尤为明显,中等城市次之。在最低等级的小城市不仅增长的趋势不明显,反而还略有下降。这种变化趋势还在不断发展中。
城市人口在年龄构成、性别构成、收入水平等方面的差别对城市经济的基本/非基本结构也都有影响。
