第二章 水文过程
2.1 地表过程:蒸发与入渗
陆面地表及准地表(subsurface)的水文过程是十分复杂的,它的类型包括植物截留、填洼、蒸发、蒸腾、入渗、下渗(到地下水)、径流、地面漫流、地下冰过程等等.其中,最为有地理学意义的是蒸发、入渗、漫流与径流.
蒸发是从液态转变为汽态的过程.在水文过程的空间尺度上,蒸发常被看作是水汽的面平均垂直对流.蒸发可以发生在任何水体表面、饱和土壤或不饱和土壤的表面,当蒸发体表面有足够水分时,由气候因素控制的蒸发率称为蒸发能力.
蒸发是影响河川径流的重要因素之一.在我国的湿润地区,年降水的30—50%被蒸发掉.在干旱地区,年降水的80—90%被蒸发掉.
太阳辐射是蒸发所需能量的主要来源.在辐射热的作用下,水从液态转化成汽态,而进入大气中.大气中的水汽在水面与上层空间形成一饱和层,只有饱和层不断地被风所移开,蒸发才得以继续.因此,风是影响蒸发的一个重要因素.当空气温度增加时,它吸收更多水汽的能力下降,蒸发速度降低.环境温度较高时,蒸发进行的较环境温度低时要快,因为环境温度较高时蒸发所需能量便于得到.另外,空气吸收水汽的能力随温度的升高而增加,故空气温度对蒸发的影响是双倍的.
饱和土壤表面的蒸发率与同等气候条件下的水面蒸发率几乎相等,当土壤逐渐干燥时,蒸发率随土壤含水量的降低而下降.根据试验可知,土壤的蒸发可分为三个阶段:
第一阶段,土壤饱和,蒸发率达到蒸发能力(同等条件下水面蒸发率).这个阶段持续到土壤含水量减至70—80%.
第二阶段,土壤蒸发率减低,大约与表土(30—50cm)层的土壤含水量成正比.这个阶段持续时间较长,直到土壤含水量减到20—30 %以下.
第三阶段,土壤表面可能结成干壳,蒸发非常困难,蒸发速度急剧减少.
不仅水面、地面、冰面存在蒸发,植物体叶面也存在蒸发.实际上,各种种类的植物都需要水分维持自己生命,植物所吸收的水分一小部分滞留植物结构中,而绝大部分植物吸收的水分,通过它的叶面蒸发到空气中.植物的蒸发过程经历了植物体内的生理反映,与其他蒸发有不同的机制,称作蒸腾,亦译作散发.
植物蒸腾量与植物种类、生长期以及供水条件等有关.白天,由于太阳辐射,植物气孔张开,因而散发量较大;夜晚,气孔闭合,散发量较小.
一般情况下,在植被覆盖区很难区分蒸发与植物蒸腾.通常是不加区分的统称为蒸发腾或蒸散发.
1) 水量平衡法
以△S代表研究体内的蓄水量变化量,I为地面入流量,Q为地面出流量,Qg为渗漏量,P为降水量,E为蒸散发量,则研究体的水量平衡方程为:
P+I-E-Q-Qg=△S
(2.1.1)
当其它各项已知时,可由上式求出研究体内的蒸散发量.
水量平衡法理论上比较简单,但实用上很难得到满意的结果,因为测量的降雨量、入流量、出流量及蓄水量变化量的误差都包含在计算蒸发量内.
渗漏量是最难估量的量,因为渗漏量只能通过测量地下水位,土壤透水性等间接估算.如果渗漏量接近或超过蒸发量,由水量平衡法难于得到可靠的蒸发量值.
2) 能量平衡法
与水量平衡法一样,研究体的能量平衡方程如下:
Qn-Qh-Qe=Qa-Qv
(2.1.2)
式中,Qn为水体吸收的净辐射(包括长波与短波),Qh为从水体输送到大气的显热,Qe为蒸发耗能,Qa为水体中的能量变化量,Qv为动水平流能量.
在天然水体中,Qh主要是通过水体表面输送的显热.该项比较难确定,通常是建立Qh与蒸发耗能量Qe间的关系.常用的关系为
![]()
式中,R为Qn与Qe的比率,P为水表面环境大气压,Ts为水体表面平均温度,Tz为高度为z处的平均空气温度,es为相应于Ts时的饱和水汽压,ez为高度z处的平均水汽压.
结合(2.1.2)(2.1.3)式得蒸发耗能量为
![]()
蒸发量与蒸发耗能量的关系为
E=Qe/ρLe
(2.1.5)
式中,ρ为水体密度,Le为蒸发潜热.将(4)式代入(5)式得到
![]()
蒸发潜热Le与水温的关系为
Le=597.3-0.564T
(2.1.7)
式中,Le的单位为卡/克,T的单位为摄氏度.
3) 经验公式法(或空气动力学法)
蒸发是水汽压差与风速的函数.因此,在应用中一般是建立蒸发量与水汽压差及风速的关系.关系式的一般形式为:
E=(es-ez)f(u)
(2.1.8)
式中,E为蒸发量,es为水和空气边界层的饱和水汽压,ez为某高度z处的实际水汽压,f(u)是风速u的函数.
当水面温度与空气温度相同时,蒸发量记为Ea,则
Ea=(esz-ez)f(u)
(2.1.9)
式中esz为空气的饱和水汽压.
4) 彭曼公式
彭曼(Penman)1948年提出了结合能量平衡方程与空气动力学法计算蒸发量的一个理论公式.
(2.1.2)式的能量平衡方程可写为
Q=Qn+Qe
(2.1.10)
式中Q=Qn+Qv-Qa.(2.1.3)式可写为
![]()
由(2.1.10),(2.1.11)式有
![]()

将(2.1.5)(2.1.8)(2.1.9)式分别代入上式得
![]()
由上式求出蒸发量E为
![]()
式中,Ea由(2.1.9)式给出,比率△/γ是空气温度的函数,随温度的增加而增加,当温度已知时,△/γ可由有关表格查出.
入渗是指水分经过土壤表面垂直向下而进入土壤的运动.它是降雨径流损失的主要组成部分.
当降水落在干燥的土壤表面时,首先受到土粒分子吸力作用被吸附在土粒周围,形成薄膜水.这种薄膜入渗又称为渗润.当土壤中的薄膜水得到满足后,入渗水就填充于土粒之间的小孔隙里形成弯月面.弯月面上由于水分表面张力的作用,具有毛管力,弯月面曲度大,毛管力也大.毛管力使水分向土隙狭小处移动,这样,土中较小孔隙首先被填满,而较大孔隙还没有填满,这种毛管入渗又称为渗漉.当表层土中的毛管充水满足后,若地表仍有积水,则继续入渗的水分填充较大的孔隙,首先使表层土含水量达到饱和.此时,饱和层毛管力的方向向下,水分在毛管力作用下向下层运动,同时,孔隙中的自由水因重力作用也沿孔隙向下流动.此后,若地面继续供水,则土壤饱和层不断扩展,使饱和层和下层之间形成一湿润层.湿润层内土壤含水量向深层递减,湿润层的前缘称为入渗锋(面).若地面雨水消失,则入渗过程结束.观察发现,随着饱和层向下延伸,促进入渗的毛管力也逐渐减小,故入渗速度也随之递减,至入渗面达到一定深度后,水分在重力作用下运动,入渗速度趋于稳定值.
R.E.Horton于1933年实验发现,入渗率随入渗时间的变化关系可由下式表示
f=fc+(f0-fc)e-kt
(2.1.15)
式中,f为入渗率,f0为初始入渗率,fc为稳定入渗率,k为与土壤性质有关的常数.通常k是土壤表面组织的函数.如果土壤表面植被较好,则k植较小,反之,R值较大.这里的f0和fc是土壤类型和土壤覆盖的函数.例如,对裸露的沙土或砾质土f0和fc较大,而对裸露的粘土f0和fc较小.
土壤类型、含水量、土壤中的有机质、植被等都对入渗有影响.在土壤孔隙中,非毛管孔隙率是最主要的因素.孔隙率决定了土壤的蓄水量,因而影响水流阻力.因此,入渗率随孔隙率的增大而增大.有机质的增加也使入渗率增大,主要是因为有机质改变了相应的孔隙率.
入渗过程是土壤水过程.设土壤是刚性的各层同性而且等温,入渗的水体是不可压缩的,则水的流量满足达西(Darcy)定律:
![]()
这里φ为水力势,它是压力势ψ与重力势的和.在非饱和土中,ψ≤0,K是水力传导系数,在土壤水份未饱和的情况下它是ψ的函数,q是土壤水流量.
在土壤中含水量θ的变化应等于输入与输出水量的差
![]()
结合(2.1.16),(2.1.17)即得土壤水运动方程
![]()
在一维的情况下并取饱水面z=0,向上为正,(18)可写作
![]()
为了求解入渗或其他土壤水过程,需要补充“本构”关系和状态关系,特别取
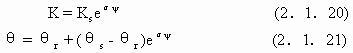
则可将(2.1.19)化作线性方程
![]()
这里Ks是饱和水水力传导系数,θr是滞留水含量,θs是饱和含水量,均为常数.
一般的入渗问题,其边界条件是(取饱水面为z=0,z方向向上)
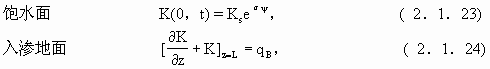
初始条件为
![]()
式中,L是土层中未饱和层厚,ψ0是饱水面水力势(水头),qB是入渗量,qA是由于ψ0产生的初始土壤流.
Srivastava和Yeh(1991)基于(2.1.22)—(2.1.25)采用拉普拉斯变换求解了均质土壤层的情况得到
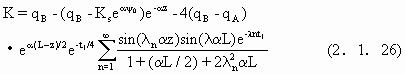
式中
![]()
相应地可以求得z=0处(饱水面)上得到的渗入量
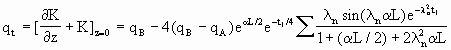
(2.1.28)
(2.1.27),(2.1.28)表明入渗量随时间指数衰减.
土壤水运动方程还有另一种表述.实际上由(2.1.19)式可得
![]()
![]()
![]()
![]()
(2.1.30)式被经常地用于分析土壤含水量的变化.Philip(1991a,b,c)基于(2.1.30)式求解了地面水量为θ1的坡面下渗过程.Philip处理下渗为初边界问题
![]()
这里θ0是初始土层含水量,θ1是表层含水量,z*是垂直坡面定义的坐标,对斜直坡来说,如坡度为γ,则将x,z化作
x*=xcosγ
(2.1.34)
zx=-xsinγ+zcosγ
(2.1.35)
对应的斜直坡方程为(注意sinγ~0,对于小角度坡成立)
![]()
关于初边值问题(2.1.32),(2.1.33),求解(2.1.36),Philip得到坡面上的正交于坡面的入渗率vn和入渗的总量in分别有近似解:

特别有

即对于垂直分量来说有

式中,S,A,K,K1是与土壤性质有关的常数,Z与含水量θ有关.采用类似的方法,Philip(1991b,1991c)还得出了凹凸坡、圆坑、圆丘的入渗规律,并发现入渗存在水平分量.这些关系的重要性在于发现经一段时间后,坡面入渗趋于定值.
Wallach等(1991)求解了一个起伏地面上入渗分布不均匀的稳定流下渗问题,这时仍取z向上为正,但z=0取在起伏地面最凹处,水动力方程为
![]()
![]()
得线性方程
![]()
边界条件为
K(y1,y2,L)=S,当z=L
(2.1.46)
和
![]()
(2.1.47)
这里L是饱水线深,S是常数,F是地面起伏,f(y1,y2)是在地面上的入渗分布,y1,y2是地面坐标方向.Wallach等以摄动方法求得K/Ks的零级近似为
K0(y1,y2,z)=f(y1,y2)+[S-f(y1,y2)]exp(z-L)
(2.1.48)
(2.2.48)式指出,在稳定入渗的情况下,水力传导系数是指数上升的.K值求出后即可估算入渗情况.
2.入渗的动力学
2.1.2 入渗
1.物理图景
2.蒸发量的估算
2.1.1蒸发与蒸腾
1.物理图景
