2.3 海洋水文过程
海洋水文的内容可以是十分广泛的.由于海洋的广阔,海水的运动中受制于地球表面特点已经可以忽视,故海洋水文过程更多呈现为“纯”物理问题.理论地理学限于研究近岸地带的问题;在这一地带海水的运动,或多或少受到地域作用.
海水是一种流体,因此,它的动力学过程服从一般的流体力学方程.由于问题的不同,常对原始的复杂的流体力学方程作各种简化,而潮波、近岸环流被用浅水模型加于研究.
2.3.1 波浪
波浪运动可以简化作xz平面上的二维运动,这时流体力学的连续性方程为
![]()
在重力作用下的无旋无粘流体适合于
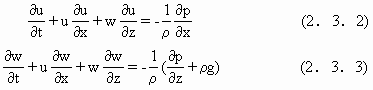
这里u和w分别表x方向和z方向流速,p为水头压力,g为重力加速度,ρ为流体密度,z坐标定义向上,取φ(x,z)表示流体的速度势,即

在假设流动过程是无旋运动的条件下,已经导出(Newman,1977,pp102-109)
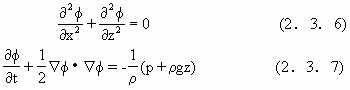
(2.3.6),(2.3.7)式分别为拉普拉斯(Laplace)方程和伯努利(Bernoulli)方程,这是描述波浪运动的基本方程组.
记η为表面的波动量,即波动表面对静止水面的偏离量,显然求波浪运动就是求η的变化.在波动表面是自由的条件下,设波动振幅较小或者流体质点流速(不是波速)很小,可以进一步得到动态边界条件(Newman,1977,p.239)
![]()
对自由表面来说,水面流体压力应与大气压力平衡,故可以设P=0,从而得到
![]()
注意到取静止表面为z=0,则有η=z,从而有
![]()
![]()
面满足
![]()
严格地讲,(2.3.11)式是关于表面的,但由于我们仅考虑小振幅波,故认为它对z=0的邻域均成立.
设波动具有一般平面波的形式,即取
φ(x,z,t)=Re[Y(z)e-i(kx+ωt)]
(2.3.12)
代入φ的方程,得
![]()
Y有通解
Y=Cekz+De-kz
(2.3.14)
在水深无限的条件下,z→-∞,Y要求有限,必须D=0,结合边界条件
![]()
![]()
这里A是某一常数,这个解表明,振动向海底指数形衰减,将(2.3.15)式代入(2.3.11)式,得到
k=ω2/g
(2.3.16)
又由相速度的定义C=ω/k,易得
C=(gλ/2π)1/2
(2.3.17)
这里λ是波长,由定义知λ=2π/k.(2.3.17)在地貌学分析中经常被引用.
地理学更多地考虑近岸带有限水深的环境,当深度h处有一个不可渗透底,在底上流量垂直分量应为0,故有新的边界条件
![]()
这(2.3.14)式中的D可以不为零,类似于前面的推导,注意(2.3.18)式,容易得到
![]()
将(2.3.19)式代入(2.3.11)式得到
kth(kh)=ω2/g
及 C=[(g/k)thkh]1/2
(2.3.20)
进一步地由φ的定义,可得流速
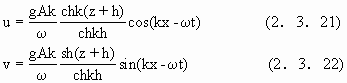
![]()
![]()
(2.3.23)式与(2.3.20)式的主要差别在于(2.3.23)式描述的,波浪是非色散的,也就是说在近岸浅水带,波浪的波速与波长无关.
式(2.3.21),(2.3.22)是关于质点速度的,将它们关于时间积分,可以得出半个周期内流体质点位移量近似为
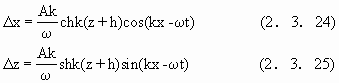
这就表明波浪运动水质点轨迹在浅水区是一个椭圆,在z=-k的海底,△x不为0,对海底有切向拖曳作用,这对于海底的泥沙运动具有重要意义.上述结果主要是由Airy在19世纪完成的,故称为艾里波理论,由于它仅考虑线性项,又称线性波理论.
如果考虑在水面自由边界,压力是个常数,那么有Dp/Dt=0,由
![]()
这里引用了导算子D/Dt的定义,得出一个非线性方程
![]()
由(2.3.27)求出的φ比线性近似时多出一个阶为O(A3)的项,近似地在深水条件下有
![]()
最后一项修改了波动剖面,它使得波峰变得尖锐而陡峭,波浪剖面呈相交的凹曲线形态,不再是正弦曲线.
对波浪运动引入类似于小振幅,有限水深的其他一些假设简化波浪运动方程(2.3.6),(2.3.7)或者连续方程和动量方程,可以导出另一些形式的波浪运动的解析近似.比较著名的有斯托克斯(Stokes)波、孤立波和椭余波(又称Cnoidal波).前者适合于有限深度波浪小而波高有限的情况,这时波剖面可被描述为
![]()
(2.3.29)
相速为
![]()
孤立波适合于浅海近岸地区,它的波剖面和波速分别为
![]()
(2.3.31)
![]()
(2.3.32)
![]()
为u=Cη/(h+η),向传播方向有净的水量输送.
与孤立波有类似环境条件的是椭余波,实际上孤立波是椭圆余弦波的一种波动周期为无限大的特例.椭余波的波剖面为
![]()
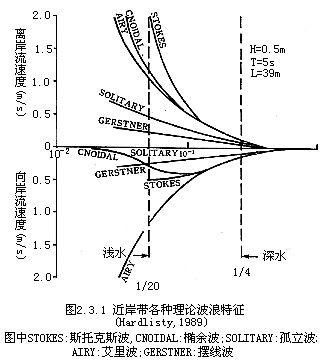
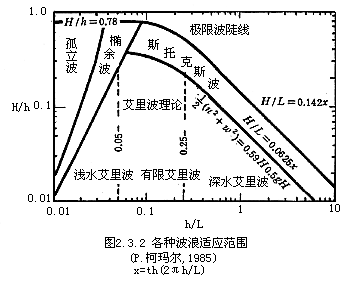
式中,K(k)是第一类模数为k的完全椭圆积分,而η是在水平坐标x处,波谷面以上的垂直坐标,cn(r)是r的雅可比椭圆函数.图2.3.1是近岸带各种波浪理论波峰的流速,图2.3.2是各种波动理论适用的海洋环境范围.
波浪问题的讨论,给我们一种强烈的提示,波浪问题,已经不依赖于地域,它具有“纯”的物理特征.所以,严格地讲,对波浪的研究,已经不属于地理学领域.但是由于地球表面波浪与其他地表圈层的相互作用是经常的,所以我们需要对波浪理论作适当的了解.类似地问题还有潮汐、大洋的环流等,关于它们的理论可以参见有关参考书如陈宗镛(1980),Pedlosky(1979).
2.3.2 潮 波
在近岸地带,海水相对变浅.所谓浅是相对尺度的,天体运动引起的潮汐现象其波长是全球尺度的,所以相应的“浅水”范围比上节波浪的浅水范围要深.其次,潮汐及其产生的潮汐尺度的宽广,使我们在分析它的运动时,不能不考虑地球自转产生的科里奥利力的作用.在这种条件下,一般取浅水方程描述海水的运动
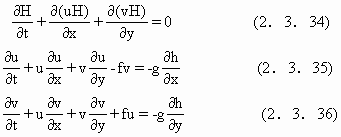
其中h为水深,u,v分别为x,y方向的流速,g为重力加速度,H为运动流层厚,近似地h也可取作H,f为地转偏向力.
![]()
这里的Ω为地球自转角速度,φ为纬度.在第一章中,我们已经知道,(2.3.34)与(2.3.35),(2.3.36)分别为连续方程和动量方程.
![]()
+η,这样可得线性方程
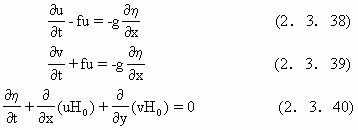
这是利用数值方法求解浅海水流问题的基本方程,这组方程可进一步地化作
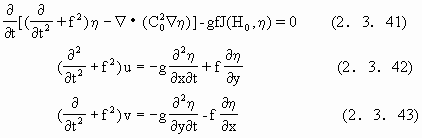
式中
![]()
J(A,B)是两个函数的雅可比
![]()
在上述方程中仅考虑了地转偏向力的作用,如还存在风力拖曳等,则应在(2.3.35),(2.3.36)或(2.3.38)、(2.3.39)中加上相应的项,潮波问题不存在相应的项的.
潮波是一种波动,类似于波浪的处理,我们可以取它的解为
![]()
k,l分别是x,y方向的波数,ω为角频率,φ为相位,将它们带入浅水条件下的(2.3.42),(2.3.43)式,可以得到u和v.平行于波动传播方向的分量u∥和垂直于波传播方向的分量u⊥
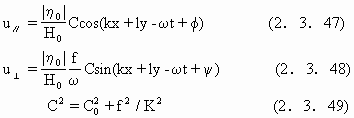
这里C是波速,K2=k2+l2.由此可得到
![]()
即知有限深水域的潮波波速矢量以一个椭圆形式在空间转动,其方向是左旋的.注意到(2.3.49)式,我们可以发现潮波传播速度比相应的“波浪”速度C0=(gH0)1/2来得快,与地球纬度有关.
更常见的地理问题是在海峡、河口、海湾一类地理环境中的潮波,先考虑无限长的平坦的海峡或海口,海岸(河岸)限制了海水的运动,在海岸处,y向速度必须为零,水深为常数H0,这就得到边界条件和控制方程
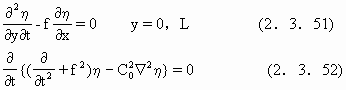
L为海峡宽,以
![]()
![]()
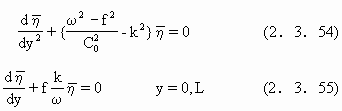
其通解为
![]()
![]()
αA+fkB/ω=0
(2.3.57)
![]()
(2.3.58)
这里一组齐次线性方程,A,B均不为零的条件是
(ω2-f2)(ω2-C0k2)sinαL=0
(2.3.59)
![]()
(2.3.55)的三个解.其中有重要意义的是ω=±C0k的解,这一解为
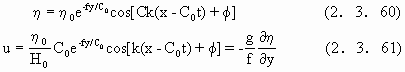
这种波动称为Kelvin波,它使得海峡中出现往复流,并且产生与科里奥利力平衡的指数型倾斜的水面,面对传播方向,右侧水位高出左侧.对应于sinαL=0的解,得到
![]()
的一系列波动,u,v分量均不为零,ω2=f2的解被发现不能同时满足两个边界条件.
如果认为海峡底向一侧倾斜,即
![]()
![]()
于Kelvin波的讨论,可以得到
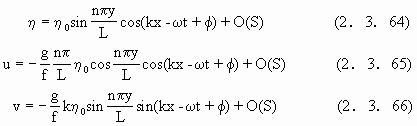
特别是它沿x方向的波相速是负的,即
![]()
这种波称为Rossby波.Rossby波不仅在浅海中,而且在大气中都是种重要的波动,因此对它的性质作了众多的讨论,部分内容可参见Pedlosky(1979).
限于篇幅,潮波的内容我们就讨论这些,进一步的内容乃至于潮汐理论、分潮理论,可以在陈宗镛(1980)的著作中找到.
2.3.3 其他
1.近岸环流系统
近岸环流是由于表面风力拖曳产生的,所以近岸环流研究中需要考虑水的粘滞性、可压缩性和热力学性质.同时考虑到上下水层之间作用,在研究中,边界层理论经常地被引用,因此,参数化方法被作为重要的手段用于研究近岸环流系统.这里我们用两个例子来说明这种研究的特点.
1) Dalu-Pieke的例子
Dalu和Pieke(1990)建议用下列方程来研究风生环流问题.
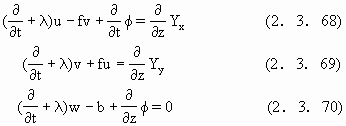
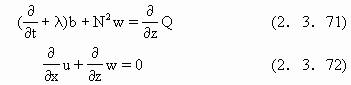
这里f是科里奥利力(地转偏向力),b是热浮力,φ是压力,λ-1是阻尼因子,λ反映了水的可压缩性,这里的写法隐含可压缩流体的振动以e-λ为衰减因子,Y是风的切应力,Q是由蚀变产生的热浮力,Y和Q被
![]()
率,表征海气温度梯度变化产生力学效应.
![]()
这里θ是大气位温.定义流函数为
![]()
(2.3.68)-(2.3.72)可化作
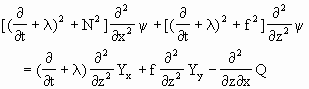
(2.3.75)
Dalu等用参数化方法和拉普拉斯变换求解(2.3.74)式,其中Y,Q等是以参数化方式处理的.
2) Poon和Madsen的例子
Poon和Madsen(1991)对风生环流的研究属于近岸环流研究方法中的另一种类型.他们考虑海水为两层的,η≥z≥h1为第一层,-h1≥z≥h2为第二层.对每一层的流速作积分得连续方程和动量方程如下:
![]()
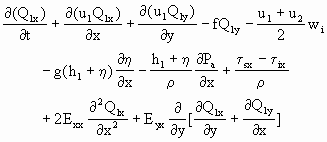
(2.3.77)
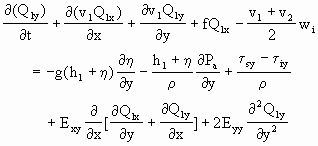
(2.3.78)
![]()
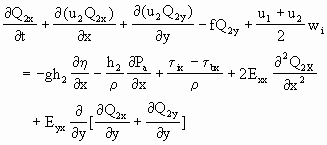
(2.3.80)
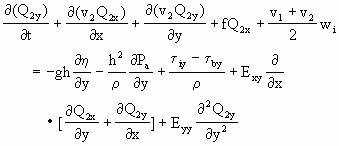
(2.3.81)
式中,Qkx,Qky是水体在x,y方向的流量,uk,vk分别是层k中x,y方向的深度平均流速,f是科里奥利力,wi是内层面上的交换水流流速,Eij是涡旋粘滞系数,τsx,τsy分别是水面上x,y方向的切应力,类似地τbx,τby,是海底切应力,τix,τiy是内界面切应力,η是表面起伏,Pa是大气压力,ρ是液体密度.为求解,切应力被引用边界层理论参数化为

![]()
这里ρa是大气密度,ua,va为x,y方向风速,Cd,Cb分别为气-水
![]()
这种多层模式方法,取每一层具有均匀的性质,有利于参数化,使得问题简化.在某些假设下,可以将部分方程化作代数方程,从而使求解变得容易.对微分方程的数值求解,也常因分层-参数化的方法,使问题的线性增加,从而可能使计算稳定和简化.因此,在对地球表层各圈层流体运动和圈层相互作用时被大量地采用,在大气模式中,多数模型发展为多层模型.
2.盐水楔
在河口地区,上游来水与海水交汇,形成淡水浮于上层,咸水楔入的盐水楔.在海岸地下水中,海水渗入含水层,上游淡水地下径流被咸水浸染,也形成地下水的盐水楔.河口盐水楔一般用欧拉方程求解,地下水盐水楔,也满足地下水的运动定律,这时用达西定律代替动量方程,与一般水文问题不同.盐水楔研究有两种模型:其一是界面模型,假设淡水为上层,咸水为下层,形成一个楔状界面,上下层之间相互作用为拖曳作用,建立两层各自一组方程.第二种模型为弥散模型或称浓度模型,它从盐分分布于水中的事实出发,不假设界面存在,而认为盐分含量应是逐渐过渡的.基本水量平衡和盐分平衡,分别建立二个连续性方程,在动量方程中则考虑盐分的扩散作用,后一种模型主要用于研究海岸地下水浸染的盐水楔.由于盐水和淡水为不同的物理化学相,近年来,两相流方法被用于研究盐水楔问题.其次,由于盐水楔位置具有一定的
![]()
下面的两个例子试图说明盐水楔研究的特征.
1) 稳定流——河口盐水楔
已经有众多的作者研究了一个稳定的盐水楔形态问题,他们的模型是界面模型.设淡水层满足连续性方程
![]()
动量方程
![]()
这里下标1标注上层(淡水层)特征量,τi为淡水层内切应力,u1,w1分别是x,z方向流速,h为水深,ρ1为淡水密度.沿z方向积分上式得
![]()
(2.3.89)
这里τs,是表面切应力,对式(2.3.89)取平均,并取u1(x,z)=u1(x),得
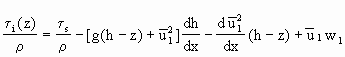
(2.3.90)
式中上横号表示层平均.沿z上层内积分得
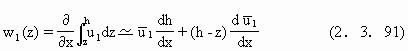
合并(2.3.90),(2.3.91)得到
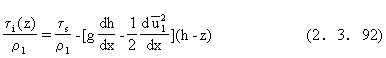
以边界层公式代替τ,并作若干简化,特别是取界面切应力τi=ρCu2,u是上层水体平均流速,以盐水楔顶为x=0,得到盐水楔界面hi满足
![]()
(2.3.93)
这里盐水楔剖面由Farmer和Morgan于1953年求得.这里H为总的水深,F0为弗劳德数,如设界面切应力τi和水底切应力τb分别为

进而求得
![]()
(2.3.96)
这里求得的结果与时间无关,是稳定流条件下的界面(Sorgard et al.,1991).
2) 二相流——海水浸染
设海水浸染地下水形成上下两层间存在界面的盐水楔,淡水相和咸水相分别为上层和下层.在地下水中,基本的不可压缩流方程这时分别满足
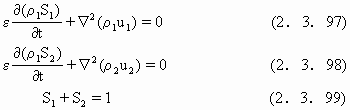
式中,ε为孔隙率,ρ1,ρ2分别为淡水和咸水密度,u1,u2分别为上下两层的平均流速,S1,S2分别为淡水、咸水饱和度,ui满足达西方程
![]()
压力之间存在压容关系
p1-p2=pc(S2)
(2.3.101)
这就是海水浸染地下水的两相流模型,这个模型由Ledoux等(1990)建议,它只能用数值方法求解.两相流方法用于河口盐水楔的研究方面,笔者还未见报道.
