5.2 生物学过程为主的模型
5.2.1 种群模型
1.单种模型
连续时间的无时迟的单种模型适应于种群密度分布是均匀的种群动态过程.一般地这类模型可表作
![]()
这里N是种群个体数或占地域或群落中的密度.F(N)是N的函数.如果F(N)满足以下的条件,则模型(5.2.1)是全局稳定的,即在任意干扰作用下,生态系统中该种群能保持生态平衡.这些条件是:①存在一个N*>0,使F(N*)=0,即有一个正平衡位置N*.②N*>N>0时,则有F(N)>0.③N>N*(>0),有F(N)<0.这个结论可以这样得到,
![]()
一俟N(t)>N*>0时,则由条件(3)知F(N)<0,故N<0.N(t)下降,这样N(t)→N*.同理,当N>N*为起点条件时,也有N(t)→N*.故N*就是系统(5.2.1)的全局平衡点.
模型(5.2.1)的一种具体形式是Verhulst-Pearl阻滞方程,它的意义是种群有一个“最大”密度K,当超过这个允许的最大密度时,由于种群内部资源竟争而趋于数目减少,其形式为
![]()
对应于模型(5.2.2)的种群有效增长率为r(1-N/K).显然N*=K就是相当于(5.2.1)式正平衡点.K值是由地理环境的资源量所限定的.求解这个方程,有解

式中,N0为初始种群密度.(5.2.3)式表明种群密度单调地趋于平衡点K.
地理学者关心的是种群受到人类的干扰.它或者作为资源开发,或作为“杂草”之类被抑制,这时模型(5.2.3)可修改作
![]()
u为控制变量,当u为常数时,若u>rK/4,则(4)式不存在正平衡点,也就是说系统存在“最大”,允许开发量um=rK/4.当超过这一开发水平时,生态系统不可能保持平衡,资源得不到更新.对“杂草”之类来说,必须大于um才能使杂草被有效抑制.常见的开发类型为u=EN,这里E表示了设备能力,称作作业水平(以渔业为例为fishing effo-rt),令
![]()
应满足
us=EK(1-E/r) (5.2.5)
对于更一般的开发问题,已化作了更新资源的开发问题,可参见第七章有关内容.
如果我们考虑到种群是世代更新的或者一年一次繁衍如树木,则有离数形式的Verhulst-Pearl模型,这时一般称Logistic模型
xk+1=rxk(1-xk/K) (5.2.6)
令xk/k作为一个新的变量,记作y.在上式两边同时除以K,则有
yk+1=ryk(1-yk) (5.2.7)
这是被认真研究过的方程.数学上发现,当r∈(0,1)区间,yk→0,0是不动点,种群趋于灭亡;当r∈[1,3],分叉出新的不动点,当3<r<3.57,出现周期性振动,而随r增加,依次出现2,22,23,…,7,5,3,周期.r>3.57时,系统出现浑沌.分叉与浑沌意味着生态系统的复杂性.对于更为一般的
xk+1=f(xk) (5.2.8)
来说.若x0为(5.2.8)的平衡点(不动点),当|f′(x0)|<1.x0为局部稳定的;当|f′(x0)|>1,x0为不稳定的;当|f′(x0)| =1,为临界情况(叶彦谦,1984,p24—26;陈兰荪,1991,pp.80—81).
如果考虑种群密度是依年龄分布的,一般成立著名的Sharpe-Lotke方程,它描述了种群密度年龄结构的动态关系
![]()
初边值条件为
p(a,0)=p0(a) (5.2.10a)
![]()
![]()
生率,p0为初始分布.由于它适合于描述人口过程,在人口膨胀,急需人口控制对策的条件下,方程(5.2.9),(5.2.10)被众多的学者认真地加于研究,可参见宋健(1989).
共存一个地理环境或群落中的种群之间存在复杂的合作竞争关系,这种合作竞争现象在地理系统中是普遍存在的.通过种群合作竞争,我们有可能直观地理解地理事物的其它合作竞争性.种群合作竞争的数学模型,被研究得最多的是两种群模型,在两种群模型簇中,又有若干具体模型,就其反映的物理行为来说,有一致性.我们这里讨论的是较为常见的.设N1,N2分别为种群1和种群2的数量.两种群模型为
![]()
(5.2.11)
![]()
(5.2.12)
式中,右边因子Ni表示种群的增长与本身数量呈正比,括号里的因子,
![]()
因子不再是常数而得到种群之间作用和资源数量的调节.aii<0即反映了资源的限制作用,如单种模型中因子(1-N1/K),隐含了最大资源约束的存在.不难求出系统(5.2.1),(5.2.2)有非负平衡点(负平衡点无生物学意义)

当a21>0,a12>0时,系统是一个合作系统,即种群之间是相互促进繁殖的.这时若a11a22>a12a21,则正平衡点(5.2.13),(5.2.14)是全局稳定的(Goh,1980).当a12<0,a22<0,种群之间相互抑制繁衍,系统是竞争系统,这时平衡点(5.2.13),(5.2.14)可能是鞍点,也可能是稳定结点.在第一种情形中,有一个种趋于绝灭,因此有生态意义的是第二种情形.Goh(1979)证明出现稳定结点情形的条件是K2a11<K1a21和a12a21<a11a22.注意到|a11|的意义,它相当于资源允许最大密度(单种模型中的K).这就是说,将其它种群和地理环境作为资源,仅考虑两种群竞争的情况,只有资源允许种群数量可能达到较大的量,种群才不会绝灭.当a12<0和a21>0,种群2抑制种群1,种群1促进种群2繁衍,系统为捕食者(种群2)—被捕食者(种群1)模型,这时
![]()
![]()

对于系统(5.2.11),(5.2.12)来说,在以作业水平E开发时,可以改写作
![]()
(5.2.15)
![]()
(5.2.16)
相应的生态经济平衡点为

![]()

不难求出,开采收获大于零的条件为
![]()
(5.2.19)
二种群模型的一种推广类型是食草动物与草场的模型.它也可以看作更新资源与资源开发者(资本水平)的一种关系.设H为食草动物量,g为植被更新率,V是植物量,K为最大允许植物密度,则可取系统方程为
![]()
(5.2.20)
![]()
(5.2.21)
这里(5.2.20)右边第一项实际上就是单种群(繁衍)模型.第二项描述了V受到H的控制作用,因子1-exp(-d1V)反映了草场作为资源对食草动物的供养作用,记c1为单位动物量最大食草量,c1[1-exp(-d1V)]反映了在特定的草场资源量V情况下,由于食草动物间的相互争夺,可能得到的食量水平.c[1-exp(-d2V)]则为在资源量V有限条件下,食草动物的繁衍生殖水平,c为最大生育率,a为死亡率.关于这个系统的讨论,可参见May(1981).
当系统包含m个种群时,种群模型可以表作下面的非线性常微分方程组
![]()
(5.2.22)
这里Nj是种群j的密度,ai是参数.gi的具体形式不同,将有不同的结果,Giersch(1991)讨论了(5.2.22)系统的平衡点稳定性问题.由于gi的形式不定,其结论还不能具体化.其体的gj形式,可能得出系统更为精细的行为,不过这时的分析已经相当复杂了.在三种群的情况下,系统有可能出现浑沌.地理学更关心的是种群被作为资源利用或受到环境干扰时的行为.这时(5.2.22)式应加上控制项u,特别是当靠近平衡点时.可有特殊的分室模型·(compartmental model)
![]()
(5.2.23)
当uj<0时,表示对资源系统有净的开发量|uj|;当uj>0时,表示对生态系统有输入.![]() (1990)讨论了在某些特殊条件下的(5.2.23)的行为.关于多种群的讨论,目前还带有较多的任意性,因此,我们必须注意第一节所提到的,任意地“制造”模型是危险的.模型的功能不在于解决问题,而在于发现问题.
(1990)讨论了在某些特殊条件下的(5.2.23)的行为.关于多种群的讨论,目前还带有较多的任意性,因此,我们必须注意第一节所提到的,任意地“制造”模型是危险的.模型的功能不在于解决问题,而在于发现问题.
一个群落特别是植物群落,受到地理因子的控制,即受到物理环境的作用,群落的演化与环境密不可分.最简单的情况下,我们考虑群落生物体如植株对资源的占用,资源的约束产生的群落行为.Galishy建议了一个模型试图描述植被群落的这种关系


(5.2.24)
这里B表示群落生物量,Af(t)和A(t)分别为植株自由生长所必须的资源量和群落中植物可占用的资源量.Bf表示潜在的植株自由增长条件下的群落生物量,a(B)是生物量的一个函数.可取为aBk,0<k<1,f具有性质f(0)=0, f(1)=1,0<f(x)<1(当0<x<1),可以取f(x)

等于某一常数bf,它反映了在充分自由条件下群落的更新率.实际上它是说明性的,尚少的实际解决问题的能力.
群落实际上是一个生态系统,吴建国(J.Wu,1990)建议了一群落内地生态模拟模型.其基本内容是模拟群落内气温、相对温度、辐射吸收量以及水汽、热量流与源强等.他的分析角度是动力学过程与能量平衡相结合.图5.2.1是吴建议的计算机模拟图.利用计算机模拟复杂的系统,是地生态分析的现代趋势之一.
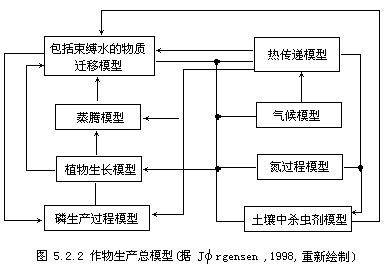
作物产量目前在两个层次上被模拟,其一是机理的地理微观的层次,其二是统计的地理宏观的层次.机理模型或生产过程的模型,追溯到了作物生产的子过程,由子过程形成的子模块相互关联,传递信息可能完
![]()
物生产过程的总模型,它一共由8个模块构成,模型的模拟,需要了解8个模块内部过程的运行机理.在实际分析中,中央的植物生产模块可能被追溯到更为细致的生理学层次.
1)作物生长模型
目前多数作者提出的干物质积累模型是说明性的.记△W为干物质增长速度,Fg为碳水化合物转变为干物质的转化率,Fs是作物同化作用产生碳水化合物的速率,Rm是相应的呼吸率,W为作物活体总干重,于是有
△W=Fg(Fs-RmW) (5.2.25)
![]()
辐射、呼吸、CO转化为组织,水的可利用性,长期水分短缺,温度营养物浓度.各种物质浓度,并且提出总同化率F(=FgFs)
![]()
式中,Fm为最大同化率,σ是效率系数,rx是羧化阻尼,C是ω2浓度.A是在波长400—700mm范围内的辐射的吸收量,单位为Wm-2时,F的单位为kgha-1h-1.他还进一步讨论了其他具体的生理过程因子,可参见原文.显然这种模型已经很难认为是地理学或生态学意义上的.我们就不多加讨论了.地理学分析中,必要时可查阅有关专业文献.
2)作物-土壤水文过程模型
a.潜在蒸腾热量方程是①

式中,Cs是水蒸汽的比热,Rn是净辐射,LE是蒸散热量损失,r是湿度计常数,h是热传导系数,ed是饱和蒸汽压,ea是叶表面蒸汽压,△则是漏热与平均气温间饱和蒸汽压曲线的斜率.
b.实际蒸发和蒸腾模型
在无作物覆盖时的最大蒸发速率Em可以假设等于潜在蒸发速率E0,在有作物的情况下,由于作物冠层的遮荫作用
Em=E0e-0.4LAI (5.2.28)
当土壤表层积水或土壤毛管水上升速率CR大于蒸发速率,而实际蒸发速率就等于最大蒸发速率.但是通常作物要求地下水位保持在一定的深度,而毛管水上升量不能完全与蒸发损失量相等,则实际蒸发量Ea为
![]()
(5.2.29)
式中,SMa是土壤风干时的含水量.
同样,在最佳供水条件下的最大蒸腾速率Tm是叶面积指数和潜在蒸腾速率T0的函数:
Tm=(1-e-0.8LAI)T0 (5.2.30)
其中T0可由彭曼公式计算的潜在蒸散速率ET0换算,易得
T0=ET0-0.1E0 (5.2.31)
c.土壤水平衡方程
RSM=[IM+(CR-D)-T]/RD (5.2.32)
式中,RSM是根系层的水分含量变率,IM是根系层上界水的净渗出率,T是作物蒸腾,RD是根系层深度,因此根系层的水分实际入渗率为:
IM=P+Ie-Ea+DS-SR (5.2.33)
其中,P是降水,Ie是有效灌溉率,Ea是实际蒸发率,Ds是表层潜水的下降率,SR是地表径流.
土壤是由固体颗粒组成的多孔介质,土壤的总孔隙度SM0由土壤容重BD和比重SD所决定
SM0=1-BD/SD (5.2.34)
![]()
示
![]()
或
![]()

![]()
其中,K0是由质地决定的饱和导水率,参数可也随质地而变化,由此式决定过渡带的导水率A.
最大入渗率由介质势和重力势共同决定,介质势的影响即为水的吸着率
![]()
式中,S0为标准吸着率.所以在实际中,最大入渗率是由介质力和重力的复合作用决定的.
![]()
即
![]()
上述土壤水运动的关系还是静态的,近年来土壤水动力学研究取得了很大的进展,水在土壤中的运动以及它与作物的关系被动态研究.在水文过程一章中我们已经了解了下渗水的动力学方程,它也适合一般的土壤水运动,可参阅该章有关内容或土壤水动力学专著.
3)土壤中物质迁移与热传递模型
土壤物质迁移主要是由水的扩散对流引起的.热传递也存在扩散对流机理.二者满足物理学扩散方程.在实际工作中,因各自的特性而取各种具体形式.土壤中物质(盐分)迁移方程常取作二维形式
![]()
(5.2.40)
式中,C为盐分含量,θ为含水量,Dxx,Dzz分别为x,y方向水的弥散系数,q为重向水(分)流量,F为源强,表示溶解盐或沉淀作用(F<0).仅有(5.2.40)式是不是于求解问题的.它还应配合于土壤水运动方程如(2.1.18)式,在有的情况下还要考虑束缚水的作用.这时在
![]()
浓度,ρ是土壤的容重.(5.2.40)式的基本形式是质量平衡,与之配合的土壤水运动方程表述水的动量平衡.
在θ=常数,q=常数时,取初值条件为 δ(x,y,0)=Mδ(x)δ(z),并设Dxx,Dzz为常数,由偏微分方程理论知(5.2.40)式的解为

(5.2.41)
这就是盐分在有土壤一个外源M作用时的分布剖面,
土壤中热传递的关系,可参阅第三章冻土一节的有关方程.
4)气候作用
气侯作用的内容从生态学水平上可能涉及两个问题:首先是光能利用率.李矩章、赵名茶(1987)建议光能利用因子Fe可估计为
Fe=ηητQ (5.2.42)
式中,Q为太阳到达地面的总辐射量,η为利用率,ητ为光量子通量密度与总辐射能量密度之间的比例参数,与波长有关,冬季(12—2月)取为0.431,春季为0.451,夏季为0.471,秋季为0.461.笔者理解这起因于不同季节大气水分,尘埃含量不一样,对太阳光选择吸收有关.
其次,地生态学一般还考虑叶面系数LAI与辐射率的关系,这种关系被更多地用于遥感估产等场合,一般认为辐射通量被吸的部分Ia与叶面指数之间存在关系
![]()
这里LAI为叶面指数,σ为散射系数,β为大于0的参数,而实验支持光合作用指标AR与图像深度指标GV可能有经验关系.
![]()
式中,a数量级为0~-1,b数量级约为-2,c数量级约为-4.
一般认为作物生产系统,宏观上具有生产水平结构,后者是由气候,土壤水分等地理因素和作物生理特征、管理水平等决定的,图5.2.3是de Wet提出的生产水平分级模式,进一步他建议了四级水平.沈思渊总结这四级水平为:

生产水平1:作物在养分和土壤水始终充足及温度适宜的条件下生长,生长速率取决于阳光辐射和作物的光能利用效率.生长期内的有效辐射量常常是限制生长速率的因子.室内试验中,某些作物可达到这一水平,如温室栽培的土豆集约化种植等.辐射强度,光的接收与利用程度,植物中能量利用效率是该水平下制约生长速率的关键因子.显然这一水平不具有直接的地理学意义.
生产水平2:作物生长至少在部分时间内受低温的影响.当温度升至适宜时,作物生长速率就增大到由光合作用决定的最高速率,例如在温带湿润地区的小麦,谷类施肥实验等.在该水平上的作物生产关键因子是作物内部生物化学过程的强度和能量转换效率.
生产水平3:作物生长至少在部分时间内受水分短缺的限制,当水分充足时生长速率就增至由气候条件确定的最大速率,例如温带半干旱地区施肥实验或大量施肥而无灌溉的大田,在这一水平上的作物生产,土壤水的可利用程度与作物对水的利用效率是关键因子.
生产水平4:作物生长至少在部分时间内受到土壤、养分缺乏的限制,在剩下的生长期内受水分或气候条件的限制.在施肥很少的农业生态系统中这是很普遍的情况,在自然界中更是常见,有时即使施肥充足,在生长期的最后阶段作物也常缺氮或其它养分.在形成实际的作物产量和植被景观时,水平4是唯一真实的.
无论哪级生产水平,农业系统的宏观产出可以看作是一系列地理因子限制作用的产物,生产水平不一样,因子选取也不一样,李钜章、赵名茶(1987)总结这些因子与产量的关系为:Yt=F(光)[F(温)∧F(水)· F(养分)· F(管理)F(前期)].这里Yt为t时期f物质产量,实际上F(管理)似应改作α+F(管理),因没有管理的原始农作系统也有产出.沈思渊(1990)系统地总结了常见的宏观生产模型,我们仅择要介绍如下:
加拿大应用的预测产量(Bra)方程取作
Bra=BnHiWMIs (5.2.45)
其中,W是水分限制应力,M是经营管理因子,Is是土壤指数,Hi是收获指数,Bn是净生物量,为
Bn=0.36bgm/(1/N+0.25Ct) (5.2.46)
式中,bgm是叶面积指数为全部覆盖时(LAI≥5)的粗生物量,N是作物成熟期的天数,Ct是维持生长的呼吸.
生物生长量正比于>10℃的积温值,而湿润系数与生物生长率呈函数关系,A.沙什科把热量与水分对生产力的影响,用生物气候相对潜力(BCP)表示如下:
![]()
式中,Kp是随热量和水分比而变化的生物生产率系数.等于缺水条件下生产率与足够湿润条件下生产率最大值之间的比值,也可用湿润系数K代替,∑t>10℃为大于10℃的有效积温,1000℃是耕地北界的积温值.
上述模型尚考虑一定的机理作用,另外一些模型则更强调限制因子的作用,从而与生产水平紧密联系在一起.Miami-Montreal模型是考虑最低限制原则的,它取
NPP=min[3000(1-e-0.000644W),3000/(1-e1.315-0.119T),
3000(1-e-0.0009696(E-20))]
(5.2.48)
式中,NPP是净初级生产力,W是年平均降水量,E是年平均蒸发量,T是年平均温.这一关系是研究地球上不同地带许多测点后得出的回归关系,在具体区域,参数需要重新估计,也可以借助某些理论分析和实验数据作出对(48)式的修改.
另外一些模型则考虑因子的综合限制作用,这方面比较著名的有黄秉维模型:
Pa=0.123QTWS (5.2.49)
式中,Pa是农业生产潜力,再乘以因子0.4就为经济产量,Q是总辐射量.T,W,S分别为温度,水分与土壤有效系数,0.123是由总辐射换算成光合潜力用干物质表示(kg/ha)的系数,由公式计算而得.赵名茶用丰产麦田的观测资料对该系数进行了检验,所得数值0.125,与计算结果一致.黄模型是由光合潜力Pf经温度、水分、土壤等因子逐级校正而得到的,可参阅原文献(黄秉维,1985).
更一般地有Olson的生物量积累模型
P=kB/(1-ekt) (5.2.50)
其中,P为产量,B是该环境下有机物的生物量,k为部分损失率.t是时间,该方程又称为单分子生长积累曲线,它可以作为回归估计的基础,也可用于分析非农作系统.Briggs等(1990)建议了一个森林生态系统生物量动态模型,他考虑的因子有潜在的蒸腾量、土壤对水的利用能力、土壤含水量及其可利用性、实际蒸腾量、截留损失、径流量、季节性变化等地理因子.由此可见,一般的林业系统生产模型类似于前述的群落模型,管理因子有时可能被忽视,依观察角度而定.
2.作物生产的宏观统计模型
5.2.3 作物产量估算模型
1.作物产量的生产模型(微观观点)
5.2.2 群落模型
3.m个种群
2.两种群模型
