1)已知原料供给地的地理分布;
2)已知产品的消费地与规模;
3)劳动力存在于多数的已知地点,不能移动;各地的劳动成本是固定的,在这种劳动花费水平下可以得到劳动力的无限供应。
在上述三种假定条件下,韦伯分成三个阶段逐步构建其工业区位论。
第一阶段:不考虑运费以外的一般区位因子,即假定不存在运费以外的成本区域差异,影响工业区位的因子只有运费一个。即韦伯工业区位论中的运费指向论。由运费指向形成地理空间中的基本工业区位格局。
第二阶段:将劳动费用作为考察对象,考察劳动费用对由运费所决定的基本工业区位格局的影响,即考察运费与劳动费合计为最小时的区位。即韦伯工业区位论中的劳动费指向论。劳动费指向论,可以使在运费指向所决定的基本工业区位格局发生第一次偏移。
第三阶段:将集聚与分散因子作为考察对象,考察集聚与分散因子对由运费指向与劳动费指向所决定的工业区位格局的影响,即为韦伯工业区位论中的集聚指向论。集聚指向可以使运费指向与劳动费指向所决定的基本工业区位格局再次偏移。
(二)运费指向论
在给定原料产地和消费地条件下,如何确定仅考虑运费的工厂区位,即运费最小的区位,是运费指向论所要解决的问题。运费主要取决于重量和运距,而其它因素,如运输方式,货物的性质等都可以换算为重量和距离。工业生产与分配中的运输重量主要来源于原料(包括燃料)以及最终产品的重量。下面从原料(包括燃料)入手,讨论工业区位的基本原理。
1.工业原料(industrial materials)的性质和重量。按原料的空间分布状况可分为遍在原料和局地原料。遍在原料即为任何地方都存在的原料,例如普通砂石等;而那些只有在特定场所才存在的原料,例如,铁矿石、煤炭、石油等则为局地原料。根据局地原料生产时的重量转换状况不同,将其分为纯原料和损重原料。纯原料即在工业产品中包含有局地原料的所有重量,而损重原料则为其部分重量被容纳到最终产品中。
运费指向论主要是使用原料指数(material index)判断工业区位指向。原料指数为产品重量与局地原料重量之比,即
![]()
原料指数大小,决定理论上工厂的区位。从上式中可知原料指数是生产一个单位产品时,需要多重的局地原料。而在整个工业生产与分配过程中,需要运送的总重量为最终产品和局地原料的和。每单位产品的需要运送的总重量为区位重量(licational weight)。

2.最小运费原理。在生产过程不可分割,消费地和局地原料地只有一个的前提下,依据最小运费原理的区位为:
1)仅使用遍在原料时,为消费地区位;
2)仅使用纯原料时,为自由区位;
3)仅使用损重原料时,为原料地区位。
这里,可以用上述的原料指数以及区位重量来得出一般的区位法则:
(1)原料指数(Mi)>1(或区位重量>2)时,工厂区位在原料地;
(2)原料指数(Mi)<1(或区位重量<2)时,工厂区位在消费地;
(3)原料指数(Mi)=1(或区位重量=2)时,工厂区位在原料地、消费地都可(自由区位)。
在生产过程不可分割,原料地为两个,且同市场不在一起时,其区位图形为一三角形,即区位三角形(图3—7(a));而当原料地为多个,并不同市场在一起,其区位图形为一多边形(区位多边形)(图3—7(b))。韦伯对于区位的推求,采用了力学方法,即“范力农构架”(Varignnon Frame)(图3-7(c))。即在给定生产1t供应市场(C)的产品,需原料产地1(M1)供应3t原料,原料产地2(M2)供应2t原料的区位三角形(图3—7(c))中,工厂区位(P)应该选择在哪里。根据韦伯工业区位论的运费指向论,工厂区位应该在运费最小地点。韦伯假定运费只和距离和重量有关,那么运费最小地点应是M1、M2和C的重力中心(图3—7(c))。


“范力农构架”可用以下公式来表示。即对于多原料地和市场的区位多边形而言,求解运费最小点即是求解区位多边形(包括区位三角形)的P点的坐标。图3-7(b)中,A1,A2,A3,A4,A5为区位多边形的各个顶点,坐标已知;假设P点为运费最小点,其坐标为(x,y),P与各点间的距离分别为ri,原料和产品的重量为Wi。那么在运费与距离、重量成比例的情况下,总运送费K可由下式来表示:
![]()
求最小值需满足以下方程组:
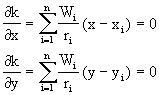
“范力农构架”(图3—7(c))就是求解上述方程组的一种模拟解法(静力类比法)。
3.综合等费用线。最小运费指向是韦伯工业区位论的骨架,可以用综合等费用线来形象地加以说明。综合等费用线是运费相等点的连线,可以图示如下(图3—8)。图中,设在单一市场N和单一原料M下,运输一个单位重量的原料,每千米需1个单位货币;而运输一个单位的产品,每千米只需1/2个单位货币;这样表示相同运输费用线将分别围绕N,M呈同心圆状。同心圆的一个货币单位的间隔就N而言,则为2km;对M而言,则为1km。这种呈同心圆状的线为等费用线。而综合等费用线则为全部运费相等地点的连线,图中A—B—C—D—E—F各点的连线,就是运费为7个货币单位的综合等费用线。A点是原料地M的2个单位,市场N的5个单位的等费用线的交点;而B点是原料地M的3个单位,市场N的4个单位的等费用线的交点,依次类推。

(三)劳动费指向论
运费随着空间距离的变化,表现出一定的空间规律性:而劳动费则不具有这种特性,它是属于地区差异性因子,它是使运费形成的区位格局发生变形的因子。
在此所说的劳动费不是指工资的绝对额,而是指每单位重量产品的工资部分。它不仅反映了工资水平,同时也体现了劳动能力的差距。劳动费主要反映在地区间的差异性上。
韦伯劳动费指向论的思路是:工业区位由运费指向转为劳动费指向仅限于节约的劳动费大于增加的运费。即在低廉劳动费地点布局带来的劳动费用节约额比由最小运费点移动产生的运费增加额大时,劳动费指向就占主导地位。对此韦伯用临界等费用线进行了分析。如图3—9中,围绕P的封闭连线即从运费最小点P移动而产生的运费增加额相同点的连线,理论上说以P为中心可划出无数条线,这即相当于图3—9中的综合等费用线。在这些综合等费用线中,与低廉劳动供给地L的劳动费节约额相等的那条综合等费用线称为临界等费用线。

在图3-9中,P为运费最小地点,劳动力低廉地为L1、L2,如果在L1、L2处布局工厂,分别比P(最小运费地点)处劳动费低3个单位。临界等费用线为标记为3的综合等费用线,因L1在临界等费用线的内侧,即增加运费低于节约的劳动费,工厂区位将移向L1处;相反,由于L2在临界等费用线的外侧,则不会转向L2处。
韦伯为了判断工业受劳动费用指向的影响程度,提出了“劳动费指数”的概念,即每单位重量产品的平均劳动费。如果劳动费用指数大,那么,从最小运费区位移向廉价劳动费区位的可能性就大;否则,这种可能性就小。但韦伯也认为劳动费指数只是判断劳动费指向的可能性的大小,而不是决定因素。因为尽管某种产品的劳动费指数高,但如果该产品生产所需要的区位重量非常大的话,也不会偏离运费最小区位。为此,他又提出了“劳动系数”的概念,即每单位区位重量的劳动费,用它来表示劳动费的吸引力。
劳动系数=劳动费/区位重量
劳动系数大,表示远离运费最小区位的可能性大;劳动系数小则表示运费最小区位的指向强。进一步也可以说劳动系数越高,工业也就会更加向少数劳动廉价地集中。
劳动费指向受到现实中各种各样条件的影响,韦伯把这些条件称为环境条件。在环境条件中,人口密度和运费率对劳动费指向的作用较大。人口密度低的地区自然地劳动力的密度也低,人口密度高的地区劳动力的密度也高。劳动费指向与人口密度相关,人口密度低的地区劳动费相差小,人口密度高的地区劳动费相差大。因此,人口稀疏的地区工业区位倾向于运费指向;人口稠密的地区则倾向于劳动费指向。
工业区位从运费最小地点转向廉价劳动力地点,取决于运费增加程度。当运费率低时,即使远离运费最小地点,增加的运费也不至于很多,从而增加的运费比节约的劳动费少的可能性就大。因此,可使工业区位集中在这个特定的劳动供给地。
综上所述,决定劳动费指向有两个条件:一是基于特定工业性质的条件,该条件是通过劳动费指数和劳动系数来测定;二是人口密度和运费率等环境条件。
韦伯同时也论述了技术进步与区位指向的关系。他认为运输工具的改善会降低运费率,劳动费供给地的指向将变强。而机械化会带来劳动生产率的提高,降低劳动系数,导致在劳动供给地布局的工业会因运费的作用转向消费地。因此,技术的进步会产生两种相反的倾向。
(四)集聚指向论
集聚因子就是一定量的生产集中在特定场所带来的生产或销售成本降低。与此相反,分散因子则是集聚的反作用力,是随着消除这种集中而带来的生产成本降低。
集聚因子的作用分为两种形态:一是由经营规模的扩大而产生的生产集聚。大规模经营相对于明显分散的小规模经营可以说是一种集聚,这种集聚一般是由“大规模经营的利益”或“大规模生产的利益”所产生。二是由多种企业在空间上集中产生的集聚。这种集聚利益是通过企业间的协作、分工和基础设施的共同利用所带来的。
集聚又可分为纯粹集聚和偶然集聚两种类型:纯粹集聚是集聚因子的必然归属的结果,即由技术性和经济性的集聚利益产生的集聚,也称为技术性集聚;偶然集聚是纯粹集聚之外的集聚,如运费指向和劳动费指向的结果带来的工业集中。
分散因子的作用是集聚结果所产生的,可以说是集聚的反作用。这种反作用的方式和强度与集聚的大小有关。其作用主要是消除由于集聚带来的地价上升造成的一般间接费、原料保管费和劳动费的上升。
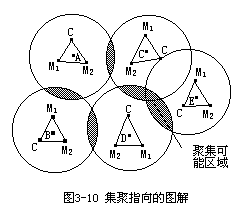
韦伯进一步研究了集聚利益对运费指向或劳动费指向区位的影响。他认为,集聚节约额比运费(或劳动费)指向带来的生产费用节约额大时,便产生集聚。一般而言,发生集聚指向可能性大的区域是多数工厂互相临近的区域。如图3—10所示,五个工厂不考虑集聚情况下的费用最小地点在图中的各处,假定当三个工厂集聚可由集聚利益使单位产品节约成本2个货币单位。为得到这一集聚利益,工厂必须放弃原有费用最小地点,从而增加运费。工厂的移动的前提必须是增加的运费低于2个货币单位。图中围绕各工厂的封闭连线,是同由集聚利益而节约的成本相等的运费增加额曲线,也即临界等费用线。在斜线部分三个工厂集聚可以带来2个单位成本的节约,并且又都在临界等费用线内侧,是最有可能发生集聚的区域。
为了判断集聚的可能性,他提出了加工系数的概念:即加工系数等于单位区位重量的加工价值。该系数高的工业,集聚的可能性也大;相反,集聚的可能性就小。
