准地转理论为观测和数值模拟得到中纬度天气系统的分析提供了重要的理论框架。原则上,在给出初始时刻的三维位势高度场之后,大气运动的三维环流及其随时间的演变,可通过准地转涡度方程和准地转ω方程预报出来,这正是准地转理论的核心。尽管准地转理论给出的预报结果,用于实际天气过程并不一定很精确,但是它可以从系统发展中分解出与地转环流部分相关的动力强迫的分量,以及其它机制如地面摩擦、非绝热加热等产生的动力和热力影响分量,进而增进对气旋等天气系统动力过程的理解。

(1)ω方程的导出及其对气旋发展的讨论
从前面涡度方程(4.40)式我们知道,涡度主要由气柱的伸缩所产生,两种最简单的情况如图4.22所示。因此,只要我们知道了垂直速度场,就可以通过垂直速度场来讨论气旋的发展问题。为此我们给出p坐标系下的准地转ω方程

![]()
(4.54)
热力学方程可写为

(4.55)



(4.56)

![]()
(4.57)

(4.58)

(4.59)
上式称为ω方程,推导中已经假定σ2在水平方向是均匀的。(4.59)式只含有空间导数,因此,它是一个用瞬时Φ场表示的ω场的诊断方程。ω方程不像连续方程,它无需依赖风的精确观测就能算出ω的值。设ω在x、y和p方向按正弦函数变化
ω=ωasinkxsinlysinmp
这里波数k、l和m定义为k=2π/Lx,l=2π/Ly,m=π/p0,Lx和Ly分别是x和y方向上的波长,p0是地面气压,m为垂直方向半波长,ωa是振幅,则(4.59)式左端可写为:

(4.60)


近,涡度平流很小(如图4.23),而在其上空高空槽前为正涡度平流,并且正涡度平流在对流层高层达到最大,于是在这个地区涡度平流随高度增加,有上升运动。在地面高压中心,涡度平流也很小,而在其上空高空槽后为负涡度平流,于是在这一地区涡度平流随高度减弱,有下沉运动。涡度平流随高度变化造成的垂直运动,其物理意义可以这样来理解:在地面低压中心1000hPa上涡度平流很小,而上空300hPa上为较大的正涡度平流。气旋性涡度增加,使风压场不平衡,在地转偏向力的作用下,必然产生水平辐散,为保持质量连续,将出现补偿上升运动,并且上升运动在对流层中层达到最大。由于这种垂直上升运动的拉伸作用,使得槽前对流层中下层气旋性涡度增加,相反地,脊前槽后则由于负涡度平流产生的下沉运动,使地面反气旋发展。
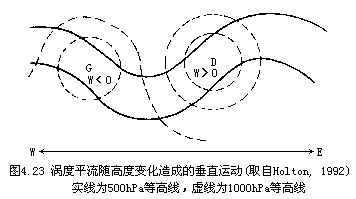

动。如图4.24中在地面低压中心和高压中心之间的高空槽中,地转风随高度逆转,为冷平流区,应有下沉运动;在地面低压中心之前,高压中心之后,高空脊上,地转风随高度顺转,为暖平流区,应有上升运动。其物理意义是槽前暖平流使高层等压面升高,使温压场不平衡,在气压梯度力的作用下产生水平辐散,为保持质量连续,将产生补偿上升运动。同理,在冷平流区应有下沉运动。由温度平流产生的正涡度变化主要位于低压中心前方,负涡度变化主要位于低压中心后方,因此,温度平流的作用主要使地面气旋发生运动。

(4.59)式右端第三项为非绝热加热的拉普拉斯项。同样
![]()

潜热时,将使上升运动加强。
在非绝热变化中,对气旋发生发展影响最大的是凝结释放的潜热。凝结潜热由上升运动引起,反过来它又加快了上升速度,这种正反馈作用往往在中层达到最大。因此,凝结潜热的释放对气旋的发展有重要作用,降水越大,这种作用越强。
地形对气旋发生发展的作用,也可通过考虑地形对垂直速度的影响来讨论。若仅考虑地形引起的垂直速度,则ω方程可写为
![]()
(4.61)
![]()
面气压,为了求出ω的解析解,设地形引起的下边界垂直速度在水平方向呈正弦分布
![]()
设上边界垂直速度为零,并设地形产生的垂直速度有如下形式解
ω=γ(p)ωp0
代入上面的方程(4.61)式,得
![]()
(4.62)
![]()
(γ)p=0=γ0=0,(γ)p=p0=γp0=1
则常微分方程(4.62)的解为

(4.63)
由此可见,地形引起的垂直速度的绝对值随气压的减小而呈指数减小。在地形尺度(L)小,稳定度(σ)大时,地形引起的垂直速度随高度衰减得快。
根据地形引起的垂直速度随高度的变化,我们可以讨论地形对气旋发展的影响。在地形迎风坡,空气被强迫抬升,由于上升运动随高度递减,涡度减小;背风坡则涡度增加。气流越山脉时发生的涡度变化,自然会对气旋的发展有所影响。
气旋东移过程中遇到较低的山脉时,在迎风坡将减弱,到背风坡会加强。如果山脉较高,则气旋在山的西侧减弱以至完全填塞,在山的东面将有一个新气旋生成。另外,在地形的背风坡容易形成地形槽,这在我国的东北平原、华北平原等地都可以看到。气旋生成频率最大的区域,几乎都在地形背风坡,这说明地形对气旋的影响是明显的。
(2)ω方程强迫项的其它形式与Q矢量
由前面的讨论可以知道,垂直运动是由ω方程中右端强迫项来决定的,对于定性讨论来讲,这种表达方式还可以接受。但是(4.59)式中,由于其右端的涡度平流随高度变化项与温度平流的拉普拉斯项中,含有较大相消项,而给分析带来误差。下面我们对这一问题进行讨论。绝热形式的ω方程为

(4.64)
![]()

(4.65)
除非在锋面和急流附近,上式中最后与变形场有关的两项数值较小,可略去它们,这种近似称为Sutcliffe近似。考虑到两层模式的热成风与热成风涡度Vg=V0+VT,ζg=ζ0+ζT,方程右端第一项展开有

(4.66)
(4.65)式右端前两项则为

(4.67)
(4.66)与(4.67)式相加并代入(4.64)式得

(4.68)
(4.68)式与Sutcliffe方程(4.47)式的形式相比,两者右端项是相似
![]()
称为引导作用项,它是地面涡度为热成风平流所产生的强迫项,是已有
![]()
是热成风涡度被热成风所平流造成的强迫作用,它对系统的加强起决定作用;最后一项则是纬度效应项,除非是大槽大脊,其作用一般较小。
由于Sutcliffe近似忽略了与地转气流变形场有关的作用项,在锋面附近可能会带来较大的误差,这是它的不足之处。因而Hoskins等引入了计算更精确,物理意义更明显的Q矢量

(4.69)
由静力关系

再根据地转关系有
![]()
因此Q矢量又可以写为

于是绝热形式的ω方程可写为

(4.70)
因此当Q矢量辐合时,可以产生上升运动,当Q矢量辐散时,可以产生下沉运动。用Q矢量除了可以推断上升和下沉运动区以外,它还可以以向量场的形式给出水平非地转运动场,此外还可以指示锋面环流的强度。这是因为Q矢量与地转锋生函数具有如下关系

可见在Q矢量与等温线垂直的地方有锋生或者锋消出现。下面是Hoskins等(1978)给出的一个例子,他们用Q矢量来诊断气旋中的垂直运动和系统的发展。如图4.25a给出1975年11月10日08时700hPa高度场和温度场,分别为实线和虚线,其中箭头所示为Q矢量,由Q矢量的长度可知道其大小,由图可以看到高空冷槽前方和地面气旋中心及其前方地区是Q矢量由大到小的地区,Q矢量在这里辐合,为上升运动,将有利于气旋发展;锋后冷空气中Q矢量呈辐散分布,为下沉运动地区。如图4.25b给出12小时后700hPa图和Q矢量的分布,图中地面气旋和高空槽已得到进一步发展,这时地面气旋中心Q矢量相当大,只是在其前方Q矢量由大到小,因此Q矢量辐合区位于地面气旋的前方,未来气旋中心将不会继续加深,而其前方的上升运动地区使气旋向前移动而不发展,锋后冷空气中Q矢量的辐散也大为减弱,这说明冷空气中的下沉运动也有所减弱。从这个例子的分析我们可以看到,用Q矢量诊断天气系统的发展即直观又方便,而且比常用的ω方程对垂直运动的诊断要可靠些。

