教学内容:九年义务教育六年制小学数学第九册70页一72页。
教学目的:
1.使学生理解平行四边形面积计算公式的来源,能运用公式正确地计算平行四边形的面积,并会计算一些简单的有关平行四边形面积的实际问题。
2.培养学生初步的逻辑思维能力和空间观念。
3.结合教材渗透转化思想。
教学重点:掌握和运用平行四边形面积计算公式。
教学难点:平行四边形面积公式的推导过程。
课前准备:投影器、长方形框架、平行四边形纸片等。
教学过程:
一、创设情境,引入新课
师:自从我校开展科技小制作活动以来,同学们做了很多精美的小制作。这是××同学制作的,大家认识它吗?
生:长方形框架。
师:如果这个长方形长3分米,宽2分米,那么它的面积是多少?
生:略
师:老师如果捏住这个长方形的一组对角,向外拉,将拉成什么图形?
生:平行四边形。
师:你们能猜出它的面积吗?
生1:它的面积不变,还是6平方分米。
生2:它的面积比6平方分米小。
师:到底哪个答案正确?相信你们学了"平行四边形面积的计算",就会茅塞顿开。
[评析:把长方形拉成平行四边形后,由于四条边的长度不变,所以不少学生认为其面积也不变。这是学生认知中的误区,教者以此为契机,创设情境,导入新知,不但温习旧知,还设下悬念,激发学生的求知欲望。]
二、动手操作,推导公式
师:(投影出示)这是画有两个不同图形的方格图(如下图所示)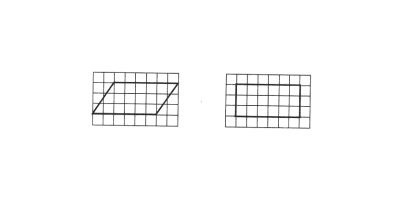
,图中每个方格表示1平方厘米,不满一格的都按半格计算。请大家看一看,想一想、议一议,可从中发现什么?
生1:长方形的长与平行四边形的底相等。
生2:长方形的宽与平行四边形的高相等。
生3:长方形的面积与平行四边形的面积相等。
师:这几位同学回答得很好!综合他们的回答,我们可以得出一个什么样的结论?
生:如果平行四边形的底和高分别与长方形的长和宽相等,那么它们的面积也相等。
[评析:让学生用数方格的方法初步感知平行四边形的面积及它与长方形面积相等的相关条件,符合小学生的思维特点,为新知学习扫除障碍,做好铺垫。]
师:刚才我们用数方格的方法求得平行四边形的面积,如果没有方格(把画有方格的投影片移开),我们能知道它的面积吗?
生:(思考片刻)能,我们把它转化成长方形就行了。
师:要把平行四边形转化成长方形,应该以什么为前提呢?
生:转化前后的面积应保持不变。
师:好!请你们拿出学具,以小组为单位边讨论、边操作,看哪个小组研究得认真,完成得快!
(学生通过激烈讨论、动手操作,争先恐后地到台上演示、发言。教师将学生演示的学具粘贴到黑板,并做适当的板书。)
生1:我们组是把平行四边形转化成长方形(图1),通量过比较,我们发现了这个长方形的长、宽、面积分别与原来平行四边形的底、高、面积相等,因为长方形的面积=长×宽,所以平行四边形的面积=底×高。
生2:我们小组是这样把一个平行四边形转化成一个长方形(图2),然后推导出平行四边形面积的算公式的。
生3:我们4:组认为,还可以沿着这条高剪下,转化成长方形的(图3),从而找到计算平行四边形面积的方法。
生4:我们小组拼成的图形跟前面三个小组不一样,我们拼成的图形是正方形。
