2．垂直速度的计算
垂直速度是一个非常重要的物理量，大气中发生的凝结和降水过程，热量和动量的垂直输送，以及大气中位能与动能之间的相互转换等，都与垂直运动有着密切的关系。它常被作为天气系统生成和发展的一个重要指标。到目前为止，还不能广泛地进行垂直速度的直接观测，只能间接计算。计算垂直速度的方法很多，最常见的有积分连续方程法和ω方程法，其它如绝热法、降水量反推法等也有一定的运用(详见第四章)。
(1)积分连续方程法
①计算方法
p坐标连续方程为
式中ω称为p坐标的垂直速度，两边对p取积分得
(2.54)
用k=0，1，2，…，9表示1000、900、800…100hPa等压面
的积分公式
……
通式为
(2.55)
式中Δp为两层等压面之间的气压差，按上述分层恒等于100hPa，如果直接采用标准等压面，这时Δp不再是一个常数。
如果已知下边界条件ω0，则可用水平散度计算任意等压面上的ωk。在地形比较复杂地区也可近似地取大气上界或对流层顶(p=0或p=100hPa)垂直速度为零作为上边界，由上向下积分，这时等压面序号可由上向下排列，(2.55)式变为
(2.56)
不过，由于高层的测风记录的误差最大，积累结果使中层的ω值更不可靠，一般很少用。
②计算结果的修正
上述(2.55)式就计算结果而言，在500hPa以下基本上正确。但由于高层风速误差比低层大1～2倍，水平散度对风的误差又十分敏感，而且由下向上计算ω时其误差是积累的，常常造成对流层顶附近仍然有明显的垂直速度，必须加以修正。修正的基本原理是补偿原理，即假定水平散度的垂直积分为零，并假定误差随高度线性增加。栗原(1961)根据上述基本设想，用
(2.57)
来修正垂直速度的计算值。式中ωk是计算的第k层垂直速度，ω′k则是该层修正后的垂直速度，ωn是大气上边界的计算值，ε(p)是权重函数，其值见表2.2。
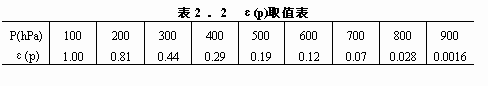
O'Brien(1970)用更严格的推证，得到目前最常用的非线性修正公式，是建立在如下推导基础上。将连续方程对p微分，得
(2.58)
如果边界条件为
p＝p0 ω0＝0；p＝pT ω＝ωT
则(2.57)式能得到ω确定的解，其差分形式为
(2.59)
式中上表“′”表示经过修正后的ω值，下表k为ω的分层序号。将上式依次写在900、800、…、100hPa层上(即k=1，2，…，9)，在
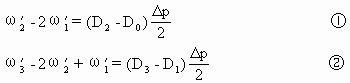
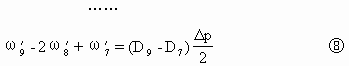
将①＋②×2＋……⑧×8，得
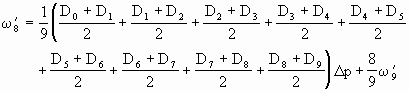
上式中
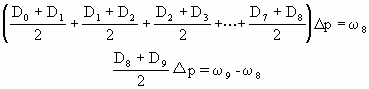
则上式变为
以同样的方法可得
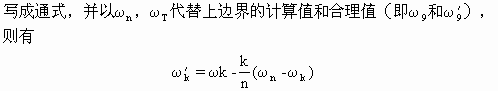
(2.60)
式中n为计算的总层次。这一修正公式的订正系数是一个k的线性函数，将这一公式分别写在k和k-1层上，则为
两式相减得
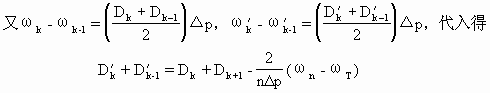
可以将此式看作以下两式的和
则通式应为
(2.61)
(2.61)式即与(2.60)式相对应的散度修正公式，其修正系数1/(nΔp)为一个与k无关的常数，这显然不符合散度误差随高度增大的事实。
如果水平散度随高度线性增加，则垂直速度的误差应是一个k的二次函数。我们仍用(2.57)式的形式将修正系数记为ε(p)，并令
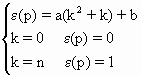
(2.62)
解之，得b=0，a=1/(n2＋n)，代入(2.62)式得
(2.63)
将(2.63)式代回(2.60)式得
(2.61)
与(2.64)式相匹配的散度修正公式能够推出
(2.65)
(2.64)式和(2.65)式即我国目前最常用的修正公式。
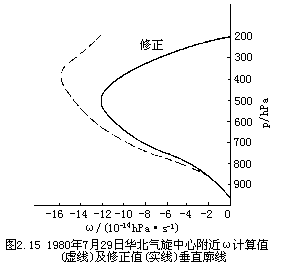
如图2.15是1980年7月29日实例计算的气旋中心附近ω垂直分布及其修正结果，修正时将200hPa取作上边界，修正结果显然比原来的合理。
用(2.64)式得到的修正系数，在以上分层中各层的值如表2.3所示，它的分布与栗原的修正系数基本相似，只是比栗原的修正系数的垂直变
与上边界的计算值ωT和合理值ωn之差有关，只是在ωn=0时，才惟一地与上边界的计算值成正比，这就比栗原的方法灵活。因为当计算层到达对流层顶附近时，可取ωn=0进行修正，但当资料不足，在200hPa以下计算时，ωn可用绝热法得到(见后面)，仍然可以进行修正。而这种情况下，已无法用栗原的方法修正。
最后，介绍一下当ω0≠0和ωn≠0时的情况。
第一，地形性垂直速度计算。
由于地表起伏可以产生空气垂直运动，因此在计算精度要求较高时，边界条件不能取ω0=0，必须考虑气流爬坡和边界层摩擦引起的垂直速度，即ω0=ωs+ωF，ωs为气流爬坡引起的垂直速度，ωF为边界层摩擦引起的垂直速度，其表达式为
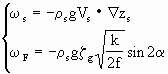
(2.66)
式中ρs为地面空气密度，取标准大气的海平面值，Vs为地面风，Zs表示地面海拔高度，ζg为摩擦层顶的地转风涡度，k＝5m2·s-1为湍流系数，α为地面风与地面等压线的交角，它随地面海拔高度而变化，为方便起见可取
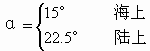
(2.67)
(2.59)式在小地形，且地表坡度比较平缓的条件下适用，但不适用于像青藏高原这样的大地形，特别是边界地形很陡的地方，这时ω可由其它方法计算。
第二，个别变化法。
当ωn≠0时，最方便的方法是用个别变化法来计算。该方法是将某种气象要素的个别微分展开，直接解出其中包含的垂直运动，故称为个别变化法。在p坐标中有
则
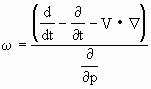
利用上式计算ω，当然最好选用在某个过程中具有保守性的气象要素。
例如，在干绝热过程中，我们可以选取位温θ(或比湿q)，则
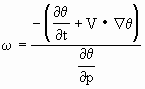
(2.68)
高度场计算；在低纬地区，如果要用高度场资料来计算，必须求解平衡方程用无辐散流函数代替风速。
因为该方法的误差不存在随高度而叠加的问题，故在对流层高层的效果较好，这是其它方法所不及的，所以常用其结果作运动学方法的上
发生时，绝热假定便不再成立，而计算的垂直速度就会产生较大的误差。以上计算公式是在干绝热条件下得到的，于是个别变化法又可称为“绝热法”。
(2)ω方程法
①准地转ω方程
这里仅给出准地转ω方程的表达式[详细推导见4.2.2中(4.59)式]
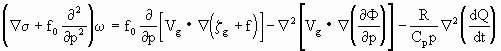(2.69)
代表静力稳定度参数。如果等式右端强迫项已知，则(2.69)式就是一个关于ω的二阶偏微分方程。
如略去σ在水平方向的变化，并引入雅可比算子，(2.69)式可改写为
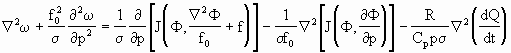(2.70)
如不计非绝热加热的贡献，或已知非绝热加热的空间分布，则只需位势场的资料，即可求解(2.70)式。但由于使用高度场计算的效果不很理想，也有将(2.69)式中关于风场的项改用实测风求解。
对于绝热过程，ω方程变为
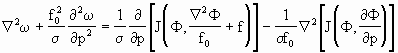
(2.71)
②平衡模式的ω方程
实际上大气运动的许多重要性质都与非地转过程有关，也就是说在一定条件下，这些非地转因子成为引发垂直运动的重要因子。Krishnamurti(1968)提出了相当平衡模式的ω方程，表达式为
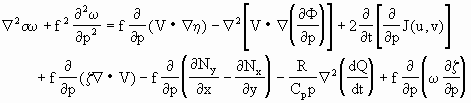
(2.72)
如果将加热函数分解为显热和潜热之和，将风场分解为旋转分量和辐散分量两部分，即令
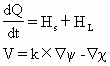
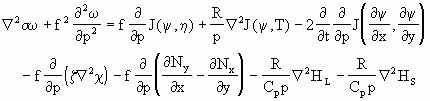
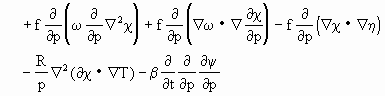
上式就是目前诊断计算中比较完整的ω方程，它的右端共有12个强迫因子，共同对垂直运动起作用。但12个因子作用的大小并不是等同的，而且其相对重要性也随时间、地点和研究对象而异。所以，为了避免复杂的计算，一般都视不同条件采用不同的简化形式。
③边界条件
求解(2.70)或(2.73)式，所用的边界条件取
其中ωs和ωF分别为地形强迫作用和边界摩擦作用。
④ω方程的求解
将(2.71)或(2.73)式右端的强迫项(有的含有ω)看作一个与公式左端未知函数无关的已知量，且σ＞0，则该式就是一个线性椭圆型偏微分方程，故可写为
(2.74)
式中Fl代表第l个强迫函数，其意义作以下简单说明：
因为强迫函数作为已知函数给出，将(2.74)式改写成差分方程，即可求得其数值解。
首先，按研究对象确定计算区域和计算网格(步长)，大尺度系统水平格距一般取200～500km，垂直格距取200hPa(如图2.16)，图中k为分层序号。输入100，300，500，700，900hPa的资料(900hPa可用插值得到)，计算输出200，400，600，800hPa等层的ω值。
其次，计算各强迫项对垂直速度的贡献：
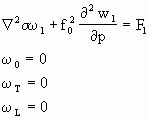
(2.75)
以k、i、j分别表示垂直方向、-y方向和x方向的网格序号，则以上微分方程可改写为差分方程
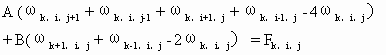
(2.76)
张弛系数，m为地图投影放大系数，d为水平格距，得Liebmann迭代解：
(2.77)
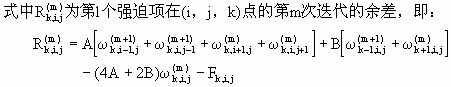
由此可以得到到ωl(l=1，2…12)。
最后，计算抬升和边界层在自由大气中引起的垂直速度(ωSF)：
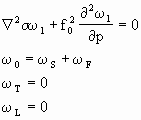
(2.78)
求得ωSF，总的垂直速度为
(2.79)
正是由于方程右端强迫项作为已知量给出，因此在求方程数值解之前，必须先确定强迫项中的ω、Hs、HL、摩擦作用、速度势χ、流函
摩擦作用主要发生在边界层，故可略去大气内摩擦。下面着重介绍加热函数、速度势和流函数的计算方法。
⑤加热函数的计算方案
(i)感热(显热)加热项的计算方案。
为求得感热加热对ω的贡献，首先要计算感热通量及其垂直分布。下垫面在单位时间内向单位气柱底面输送的感热通量按通常的半经验公式计算，即
式中CD为拖曳系数，|Vs|为地面风速，Ts、Ta分别为地温(0cm)和气温(百叶箱高度)。
由于感热向上呈线性递减，在热力混合层pu时，Su＝0，则S随高度的分布为
和
则单位时间加给气柱总热量为
该气柱中单位质量加热率应为Hs=Q/m=gS0/Δp。计算时，一般取Δp取200～300hPa，CD的取值很敏感，一般考虑它是风速的函数，即
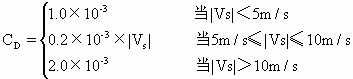
(2.80)
在高原地区，一般取CD=5×10-3～8×10-3。将感热加热率代入感热函数表达式得
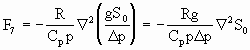
(2.81)
(ii)潜热加热函数的计算方案。
根据层结稳定度的差别，潜热加热又有两种计算方案。
第一，大尺度的稳定性潜热加热。
大尺度上升的饱和气层内，单位时间内能从单位质量的空气中凝结
(2.82)
比湿的垂直梯度。下面计算饱和比湿的垂直梯度：
因为沿局地湿绝热线上的湿静力能EP=(gz+CPT+Lqs)随高度不变，即
得
故得
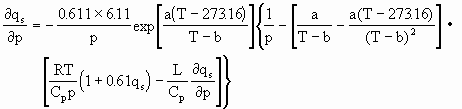
经过整理，最后得：
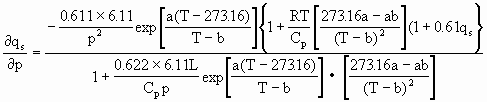
法如下：对qs=0.622E/p，E为水汽压，两边取对数并求导得
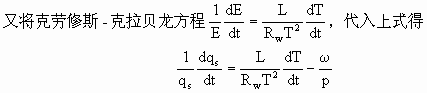
式中Rw为水汽的气体常数。在湿绝热过程中，单位时间放出潜热对外作功为
(2.83)
求取大尺度潜热加热率。
此外，由于饱和气层中稳定度必须用湿绝热线来衡量，所以，ω方程中静力稳定度参数应改写为湿静力稳定度参数σe，为了对比，将干静力稳定度参数记为σd，仿照干静力稳定度定义
满足稳定上升的饱和气层中HL＞0，否则HL=0，写成数学表达式则为
空气达到饱和时所需最低条件是根据经验估计的，不同季节、不同地区和不同高度也有差异，要在计算前加以研究确定。
第二，对流凝结加热。
对流凝结加热是在条件性不稳定大气中(σd＞0，σe＞0)，由积云对流造成的凝结释放。由于对流加热是次网格现象，无法在大尺度网格上直接计算，所以一般都采用参数化方法加以处理。积云对流参数化方法很多，大体可归纳为三类：第一类是考虑总静力能守恒的对流调整方案；第二类是考虑积云尺度质量守恒的所谓质量守恒方案。这两类方案多用于大气环流和长期数值模拟中。对于短期过程常用第三类，郭晓岚积云对流方案。
郭晓岚最先给出积云对流方案，即假设对流加热是由总的水汽辐合造成的，而水汽辐合主要来自边界层，那么它的加热量应当和边界层顶的垂直速度成正比。如果环境温度T，比湿q；积云内部温度Ts，比湿qs，则产生单位面积云柱(即设想的模式云)所需水汽量为Q=Q1+Q2，Q1和Q2分别为使云区增温和增湿所需的水汽量。它们分别用下式计算：
下标B和T分别表示云顶和云底高度参数，由于云区实际的水汽辐合I为：
式中第一项是云柱内水平幅合，第二项是通过云底的水汽流入。考虑边界层的流入是主要的，这时近似有I=-ωBqB/g。如定义Δτ表示积云生命史时间，则成云百分比面积可用a=IΔτ/Q表示，而积云对流加热率为
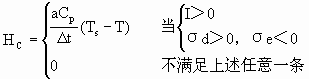
(2.84)
必须注意，计算对流加热并不需要满足大尺度场达到饱和的条件，而只需有净水汽辐合和条件不稳定这两个条件。这时，在ω方程的左则，仍需使用干静力稳定度σd。
用(2.84)式计算对流加热还需要确定云底和云顶的高度，在T-lnP图上确定很方便，在计算机上必须用迭代法求取。由于它对计算结果影响不大，实际计算中根据不同季节、不同地区取在某一固定等压面上。如一般平原上取云底为900hPa，云顶取计算上界。最后是求云内温度，在云底取云内温度等于环境温度，云底以上各层云中温度是沿着通过云底温度那一根湿绝热线而变化，所以，如以Ts(p)代表任一高度p的云中温度，那么
Ts(p)=Ts(p+Δp)-γmΔp
(2.85)
式中Δp为所取两气层的厚度，γm为以气压坐标表示的湿绝热递减率，表达式为
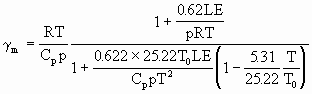
这样如果已知底层的云中温度，即可计算上层云中温度Ts(p)，再用Ts(p)计算qs(p)，代入(2.81)式求得Hc。计算中，(2.82)式中的Δp不能取得过大，常常要将两标准等压面分割成10层(10～15hPa为一层)，结果才可靠。
(2.84)式是计算对流加热常用的方法，但还存在一些不足。后来，郭晓岚作了不少改进，详细情况可参考有关文献。
⑥流函数和势函数的计算
由于水平风可分解为旋转分量和辐散分量两部分，则根据
得
这样，我们即可利用计算得到的散度场和涡度场计算流函数和势函数，计算步骤如下：
(i)将上式改写成差分方程
(2.86)
(2.87)
(ii)确定边界条件
第一，流函数的边界条件。
设边界上流函数与位势高度场之间有地转平衡关系，则边界上
另外，还可设研究区四周净质量通量M等于零，即
式中Vn是边界上风的外法向分量。在前述假定下必须将Vn进行修正，
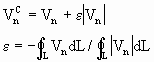
在正方形计算区四周
假设研究区西北角一点流函数已知，如ψ=0，则边界上其余点可用订正后的外法向分量即按
求解，d为格距。
第二，势函数的边界条件。
一般取边界上x=0，但如果在计算区有大地形，如青藏高原，则可利用计算好的上层势函数，用
求取地形高度以下各层地形内边界值。
(iii)用超张弛法解前述两个Poisson方程。