4.1.2 锋面结构模型
关于锋面结构认识大约开始于20世纪初的卑尔根学派的极锋模型,先后提出了不同的锋面结构模型。最早提出的锋面结构模型是所谓的楔型锋面模式(wedge model of front),有时也称不连续锋面模型;到30年代初又提出过渡带锋面模型(zone model of front);进入80年代以后,随着观测资料的时、空间分辨率的提高,又提出锋面间断结构模型。事实上关于锋面结构更仔细化的探索仍在进行中,关于锋面结构的近代许多建设性的新贡献与过去的研究结果有着惊人的相似性,而其不同点则反映在同一物理现象和动力过程的不同观点上。
下面介绍一些主要的锋面结构模型和特征。
1.楔型锋模式(wedge model of front)
所谓锋的楔型模式是指将锋面看成一种倾斜的不连续面,在锋的两侧气象要素(温度、密度、沿锋面风速等)分布是不连续的,这种不连续有时称为零阶不连续(如图4.5)。
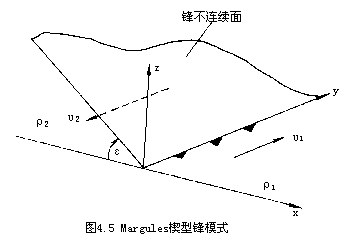
如果这种不连续面随空气移动速度传播,相应在这个不连续面上有相同空气质点组成,此时这种不连续面为物质面。在锋面楔型模式中一般将锋面看成是一种物质面。如果锋面近似为一种物质面,相应在锋面两侧无限接近的两个点,与锋面相垂直的风速分量必须相等,且等于锋面的移速,只有这样才能保证在锋面的上空质点保持不变。
在锋面楔型模式中,涡度、密度和沿锋面风速是不连续的,但锋面两侧气压是连续的。否则,在无限小的距离内,气压存在差值,这样产生一个无限大的气压梯度,这是不合理的。
最简单、最经典的锋面楔型模式是由Margules提出的,称这种模式为Margules模式(图4.5)。
在Margules模式中假定:
(1)锋面两侧的冷、暖空气的温度分别为Tc和Tw,利用Boussinesq

(2)锋区的流动平行于锋面,并假定锋面是南北方向,此条件即
![]()
(3)不考虑湍流的影响作用,这样锋面保持陡的不连续面。
在假定锋面为南北方向的情况下,描述锋区运动的方程为:
地转运动方程
![]()
4.1)
其中,ρ*为平均大气密度。
静力平衡方程
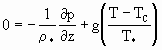
(4.2)
可利用上述方程,得到锋面的坡度。
从图4.6可知,沿任意等温线(面),有
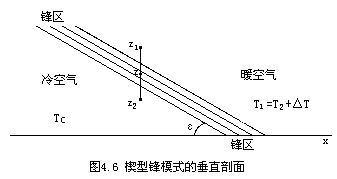
![]()
(4.3)
相应在锋区的等温线(面)的坡度ε(x,z)为
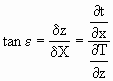
(4.4)
![]()
利用(4.1)和(4.2)式,消去p,可得
![]()
(4.5)
垂直地跨过锋区,从z2(冷区)到z(锋区)积分方程(4.5)式,得
![]()
(4.6)
利用上式,可得
![]()
(4.7)
其中,vw,vc分别为暖、冷空气的速度,上式可写成
![]()
(4.8)
这就是经典的Margules锋面坡度公式。它反映了锋面的坡度取决于锋面两侧的温差和风速切变。
![]()
(1)δT=Tw-Tc>0,锋面的坡度随着锋区冷暖空气的温差的增大而减少。当δT=0时,tanε→∞,ε=90°,即锋面成铅直,这意味着锋面不再存在。
(2)如果f>0(即北半球),相应必须有δv>0,即跨越锋面具有气旋性切变。风速切变愈大,锋面坡度也愈大;在南半球(即f<0)情况相反。
(3)如果其他条件不变,锋面坡度随纬度增加而增大。当冷锋南下,锋面坡度要逐渐减小。
楔型锋模式是锋面结构模式中最简单的模型,它具有简明的特点,它已大量应用于许多的理论研究中,但仍存在许多缺陷。
