在矢量数据结构的地理信息系统中,通常用不规则多边形来描述面状地物的区域。这样,把一幅地图中许多图斑看成许多多边形,每个多边形的边界轮廓由一条或若干条线段或弧段组成,每个弧段含首尾两个结点,每个结点连结两条或两条以上的弧段。这种数据结构形成了以面、线、点3元素组成的网络数据结构,其核心是建立各元素之间的拓扑关系,为空间数据的处理和分析提供了基础。
多边形数据的获取一般面向图幅方式,按照专题逐一进行,相应的专题数据文件结构如图3-20所示。

多边形编码系统的建立包括从数字化仪输入数据,对数据预处理,自动建立拓扑关系及生成描述多边形形状及空间关系的数据文件等,如图3-21所示。

一、数字化仪输入数据
多边形的弧段和结点数据是建立多边形编码系统的基础,通常由数字化仪输入。数字化仪输入的过程和要求,随系统不同而有差异。下面举两种方法为例子说明。
1.以结点为核心的输入法。它以图中结点所分割的弧段为单位输入坐标点数据,同时按弧段前进方向输入其左右多边形号,以帮助建立系统的拓扑关系,这种方法对输入要求严格,但自动生成多边形的工作量小。
2.以连续线段为核心的输入法。它允许用户自由选择输入连续线段的坐标点,并按每一线段只输入一次的原则输入全部线段,然后由系统对线段求交得到各个结点,分割线段、自动生成多边形,并生成相应的数据文件。这种方法对输入要求相对宽松些,但输入后,自动生成多边形的计算复杂。
二、数据的预处理
由于用数字化仪输入数据是一件劳动量很大的工作,因此,输入过程中不可避免地会出现错误,如遗漏线段,输入多余线段,弧段相交处出现如图3-23所示的过交、尖峰、未拟合点、以及悬挂线等现象;同时,输入过程中也难免会出现一些多余点。如图3-22(a)所示,图中的弧段由坐标对(x0,y0),(x1,y1),(x2,y2),……(xn,yn)组成,若其中(x0,y0),(x1,y1),(x2,y2)和(x3,y3)在一条直线上或虽不在一条直线上,但接近于在一条直线上则认为(x1,y1),(x2,y2)是多余点,应予以除去。
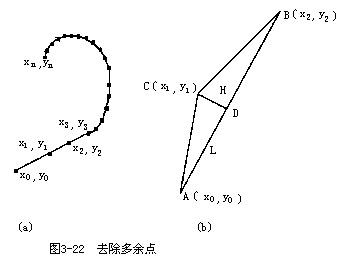
如图3-22(b)中若直线AB长度为L,点C到直线AB的垂直的距离
![]()
去除点C(x1,y1);

![]()
其中ε值为一很小值,如ε=0.001。对数字化输入的点,以弧段为单位逐点作上述处理后,可去除全部多余点,以减少数据冗余量。
结点的拟合用于去除如图3-23所示。在数据输入过程中形成的结点过交、尖峰、悬挂线等现象,实现结点拟合。结点拟合的关键是给出一个合理的容差,容差值的大小同数字化输入数据的精度有关,也同原始图件线段密集度有关。若原始图线条密集,输入弧段相交点误差很大,会出现不合理的容差值,这时应重新编辑修改输入图的数据。
对于以线段为核心输入数据的方法,通常只有少量的结点直接输入,大量的结点需要经矢量求交获取,再以结点为核心分割弧段,得到全部弧段数据。为了减少矢量求交的计算量,可将整幅图分成m×n块,逐步判断每小块内有否相交的弧段,判断直线相交关系如图3-24所示,然后进行求交。其算法如下:


当Sabc·Sabd>0时,两直线不相交。
当Sabc·Sabd=0时,两直线中一条直线的一端点在另一直线上。当Sabc·Sabd<0时,两直线相交。
2.对相交直线求出交点坐标(x,y)
![]()
该交点即为所求结点。这样对全幅图求完交点,按结点对弧段进行分割后,形成以结点为核心的弧段。
