第一节 地理空间
四、地理空间的距离度量
地理空间中两点间的距离有两种度量方法,一种沿着真实的地球表面进行,则两点间的距离除了与这两点的地理坐标有关之外,还与所通过的路径上地形的起伏程度有关,随着地形起伏的增加,距离相应延长。由于地表形态的分形特征,这种测量是十分复杂的,因此引入第二种度量方法,沿地球旋转椭球体的距离量算。它是在地理空间中相对比较遥远的两点,在假定地球是标准的球形时,两点间的距离为通过两点的地球大圆的弧长。
1.欧几里德距离
在相对较小的地理空间中,采用笛卡儿坐标系,定义地理空间中所有点的集合,组成笛卡儿平面,记为R2。定义R2中,任意两点(Xi,yi)和(Xi,yj)间的欧几里德距离d(i,j)如下:
![]()
地理空间中所有点间的欧几里德距离函数组成的度量空间记为S,度量空间具有如下特点:
(1)如i和j代表不同的点,则距离d(i,j)>0;否则,如果i和j代表同一点,则d(i,j)=0。换句话说,d(i, j)≥O的条件在欧几里德空间中总得到满足。
(2)对称性,从i到j的距离总等于从j到i的距离,d(i,j)=d(j,i)。
(3)三角不等式,给定s中的任意3个距离m,n,l,则存在如下关系式:
m+n≥l
除了欧几里德距离之外,还有其它一些空间距离度量方法。
2.曼哈顿距离
曼哈顿距离是指两点在南北方向上的距离加上在东西方向上的距离,即
d(i,j)=|xi-xj|+|yi-yj|
对于一个具有正南正北、正东正西方向规则布局的城镇街道,从一点到达另外一点的距离正是在南北方向上旅行的距离加上在东西方向上旅行的距离,因此曼哈顿距离又称为出租车距离。曼哈顿距离的度量性质与欧氏距离的性质相同,保持对称性和三角不等式成立。两者不同的是,在讨论空间邻近性时,不同点间距离的排序会有很大的不同。同时曼哈顿距离也不是距离不变量。当坐标轴变动时。点对之间的距离就会不同。因此曼哈顿距离只适用于讨论具有规则布局的城市街道的相关问题。
3.时间距离
时间距离或旅行时间距离是根据从空间中一点到达另一点所需时间进行度量的。距离关系难以用一个确定的关系式加以表达。时间距离的测量具有若干个不同尺度,包括全球尺度、国家尺度和地方尺度。交通工具的不同也影响到时间距离。时间距离不具有前述欧几里德距离和曼哈顿距离的度量空间的性质,如对称性,三角形不等式也不一定成立。在地方尺度上,常常把从一点出发到达周围特征点的时间距离值进行插值,形成等值线,从该点出发到达等值线上任意两点的距离都是相等的。在均一的地理区域里面,所有等值线应构成以该点为圆心的同心圆,而实际上的地理区域是非均质的,使同心圆结构产生变形。另外一种不同的时间距离的概念,考虑一个流域中的暴雨洪水过程,从流域上游产生的暴雨,形成径流,然后在流域末端汇流,则流域中不同位置的暴雨产流到达末端的时间是不同的。这一时间距离对于洪水预报具有重要的参考价值。
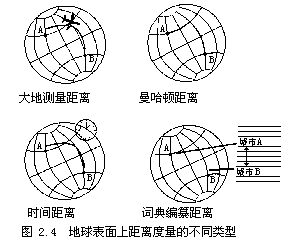
图2.4表示了地球表面上距离度量的不同类型。