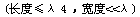针对潮汐静力理论存在的缺点,许多学者从海水运动观点出发,讨论在引潮力作用下潮汐的形成问题,建立了潮汐动力理论。
7.5.1潮汐动力理论的基本思想
潮汐动力理论是从动力学观点出发来研究海水在引潮力作用下产生潮汐的过程,此理论认为,对于海水运动来说,只有水平引潮力才是重要的,而引潮力的铅直分量(铅直引潮力)和重力相比非常小,因此铅直引潮力所产生的作用只是使重力加速度产生极微小的变化,故不重要。潮汐动力理论还认为,海洋潮汐实际上指的是海水在月球和太阳水平引潮力作用下的一种潮波运动,即水平方向的周期运动和海面起伏的传播,海洋潮波在传播过程中,除了受引潮力作用之外,还受到海陆分布、海底地形(如水深)、地转偏向力(即科氏力)以及摩擦力等因素的影响。以下主要从潮汐动力理论的基本观点出发,解释海洋潮波在几种简单特殊海区中的传播情况。
7.5.2长海峡中的潮汐和潮流
设有一个潮波传入如图7—13所示的长海峡,显然,这个潮波是沿着海峡轴线方向传播的前进波。根据前进波的性质,波峰处水质点的运动方向与传播方向相同,波谷处水质点的运动方向与传播方向相反,所以,当潮波波峰传到海峡中的任意断面BC时,BC断面皆为高潮,潮流流向与潮波传播方向相同,如图7—13中的⊙号所示,又由于科氏力的作用,使B岸的水位高于C岸;当波谷到达BC断面时,BC断面皆出现低潮,而流向与潮波传播方
![]()
于B岸。由此可引伸出长海峡中潮汐的一个普遍性质:在北半球的长海峡中,沿潮波传播方向看,右岸的潮差大于左岸,而在南半球则相反。此外,当BC断面的海面处于半潮面时,即意味着潮波的节点传到该断面,水平方向上的潮流流速为零。

7.5.3窄长半封闭海湾中的潮汐和潮流
当一个前进潮波自外海传入海湾(称为入射波)时,由于湾顶岸壁的全反射就产生了一个反射波,这两个波叠加而成的驻波构成了窄长半封闭海湾的潮波,如图7—14所示。
图7-14表示t=0、T/4、2T/4、3T/4(T为潮波的周期)各时刻入射波的波面形状(实线)及相应的反射波的波面形状(虚线),粗实线表示合成的实际潮波波面。由图可见,实际潮波为一波形不传播的驻波。离湾顶等于λ/4、3λ/4、……处为节线,在这些线上海面不发生升降,为无潮线。而湾顶和距湾顶2λ/4、4λ/4、……等处为潮差最显著的位置,被称为波腹线。
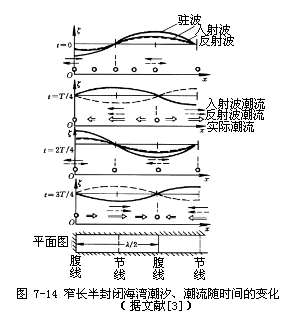
海湾中各时刻的潮流,可看作入射潮波潮流和反射潮波潮流叠加而成的。由前进波的性质可知,前进波波峰处的水质点运动方向与波向相同,波谷处的水质点方向与波向相反,节点上的水质点水平速度为零,依此可推断出各时刻入射波和反射波各处的潮流分别如图中实、虚箭号所示,两者叠加而成的实际潮流如双箭号所示。由图可见:(1)就空间而言,波腹处始终无潮流,波节处潮流最大;(2)就时间而言,高、低潮时,潮流处处为零,而海面处于半潮面时,潮流流速达最大,而此时就空间而言,波节处潮流流速最大,但波腹处潮流流速仍然为零。
现实的窄长半封闭海湾,其长度都不大于波长的1/4,其潮汐和潮流随时间变化的规律,应如图7—14中距湾顶小于λ/4的那一段所示的规律:涨潮时,潮流向里,涨至半潮面时,潮流流速最大;高潮时,潮流流速处处为零;落潮时,潮流向外,海面降至半潮面时,潮流流速最大;低潮时,潮流流速也处处为零。
上述规律可进一步定量地阐述如下:考虑一个等深的(水深为h)、长度为λ/2的窄长半封闭海湾,坐标原点取在离湾顶λ/4处,如图7—15。令湾顶低潮的时刻为t=0,则海湾潮位ζ的表示式为:
ζ=αsin(2πx/λ+2πt/T)+αsin(2πx/λ-2πt/T)
=Asin(2πx/λ)cos(2πt/T) (7—26)
它表示一驻波,是入射波和反射波的叠加,式中A=2α为驻波的振幅。
式(7—26)描述了波面(图7—14粗实线)随时间的变化。在x=0、λ/2处,sin(2πx/λ)=0,即距离湾顶λ/4,3λ/4处是无潮线。在
![]()
潮差最大,该处为波腹线。为了解窄长半封闭海湾潮流的量值及分布变化规律,引用海水连续性方程可得潮流:
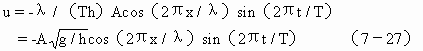
由式(7—27)可知,对于距湾顶小于λ/4的范围之内,潮流具有以下特征:
(1)当t=0或T/2时,即湾顶处于低潮或高潮时,sin(2πt/T)=0,因而u=0,潮流流速处处为零。
(2)当t=T/4或3T/4时,即海面涨至半潮面或退至半潮面时,就流速的时间变化而言,此时sin(2πt/T)=±1,则:
![]()
潮流流速的绝对值达最大,涨潮时t=T/4,u为负,流向向里;落潮时t=3T/4,u为正,流向向外。此时就空间分布而言,在x=-λ/4(即在湾顶)处,u=0;而在x=0(即在距湾顶λ/4)处,cos(2πx/λ)=1,所以
![]()
表明该处流速最大。但一般海湾的长度远小于λ/4,因而不会出现这么大的潮流。例如某窄长半封闭海湾的水深约15m(可计算得到正规半日潮潮波的波长约为540km),湾口离湾顶约25km,潮差2A=6m,由式(7—28)可得该湾口(即χ=-(135-25)km处)的最大潮流速度为0.7m/s。
应用式(7-26)和(7-27)进行潮位、潮流流速的计算时需要注意:(1)式中x的起算点是坐标系的原点,若x′表示某地P离湾顶的长度,则x=(x′-λ/4);(2)t=0的时刻为湾顶的低潮时刻;(3)ζ表示的是潮位,若要求潮差,则应先求最高和最低潮位后,再相减即可得;(4)ζ的起算面取在平均海平面。
7.5.4半封闭宽海湾中的潮汐和潮流
浅海中半日潮波的波长大约为1000km(如水深h=60m)。以下研究一个宽度与潮波半波长相当的半封闭海湾的潮波传播特征。
一、定性解释
设北半球的半封闭海湾,其长度和宽度都等于潮波波长的一半,有一个前进波沿BD方向传入该海湾,见图7—15。如上所述,由于湾顶的反射必形成一个沿海湾轴线BD起伏的驻波。在湾顶从低潮上涨到半潮面(令此时t=0)的过程中,各处的潮流方向指向湾顶,由于科氏力的作用,使海水有向右的流速分量,引起海水在右岸(面向湾顶而言)堆积。当t=0时,BD线处于半潮面,各处BD方向的流速达到最大,右岸海水的堆积也达到最高,而左岸海水流失最甚,此时的流速分布和海面形状如图7-15D所示。
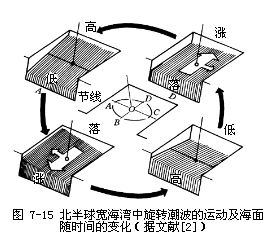
t>0以后,湾顶水位继续上涨,湾口水位下降,BD方向的潮流流速逐渐减弱。当t=T/4时,湾顶处于高潮状态,而湾口处于低潮状态,BD方向的流速为零,另一方面,在t>0以后,由于BD方向的流速减弱,右岸指向左岸的压强梯度力大于科氏力,使海水从右岸向左岸流动,在t=T/4时,AC线处于半潮面,从右向左的流速达到最大,此时的海面形状及流速分布如图7—15A所示。
t=T/4过后,沿纵断面(指与BD断面平行的断面)起伏的驻波使湾顶水位下降,湾口水位上升,并且发生退潮流,在科氏力的作用下,使海水向左岸堆积。t=2T/4时,BD线处于半潮面,左岸处于高潮状态,右岸处于低潮状态,水位和潮流分布如图7—15B所示。
t=2T/4过后,湾顶水位继续下降,湾口水位上升,退潮流流速减弱。t=3T/4时,退潮流流速为0,湾口水位达到最高,湾顶水位最低。在流速减弱过程中,由左岸指向右岸的压强梯度力大于由右岸指向左岸的科氏力,使海水从左岸向右岸流动。直至t=3T/4时,AC线处于半潮面,沿AC方向流速达到最大,水位和潮流分布如图7—15C所示。
综上所述,可以看到外海传入的潮波不仅引起一个沿“纵断面”起伏的驻立潮波,还引起一个沿“横断面”起伏的驻立潮波。两断面相互垂直,而且后一个驻立潮波的位相比前者迟T/4。宽海湾的潮汐和潮流就是这两个驻波叠加而成的,其中沿“纵断面”(即BD断面)的驻波是由于外海的潮波传入湾内后因湾顶的反射而产生的,另外一个沿“横断面”(即AC断面)的驻波是由于地转效应(即科氏力的作用)引起海水的堆积与流失而产生的。
二、定量结果
考虑北半球一个等深h,长、宽相等且等于λ/2的半封闭海湾,坐标原点取在湾的中心(如图7—16所示),令湾顶低潮的时刻为时间t=0(应注意此处的初始时刻与定性解释时的假设不一样)。

1.潮汐假定海湾里的潮汐视为振动平面相互垂直、位相相差π/2的两个驻波的叠加,于是可得到该海湾潮位的表达式:
ζ=Asin(2πx/λ)cos(2πt/T)+Asin(2πy/λ)cos[2π(t-T/4)/T]
=A[sin(2πx/λ)cos(2πt/T)+sin(2πy/λ)sin(2πt/T)]
(7-30)
当x=0且y=0时,即在原点处,潮位ζ恒等于0,所以,该处为无潮点。由
![]()
tan(2πt/T)=sin(2πy/λ)/sin(2πx/λ) (7-31)
也就是说,于时刻t出现高潮或低潮的点(x,y)必须是满足式(7-31)的点。
例如在t=T/8时刻,由式(7—31)可得此时tan(2πt/T)=1,那么:
sin(2πx/λ)=sin(2πy/λ) (7-32)
即此时出现高潮和低潮的位置在AB线上(见图7-16,AB与0x成45°角)。又从式(7—30)可知:在0B线上,ζ为正,0B出现高潮;在0A线上,ζ为负,0A出现低潮。
当t=T/4时,tan(2π/T)→∞,即sin(2πx/λ)/sin(2πy/λ)→∞,高潮发生于0C线上(图7—16)。
于是可得:对于北半球的半封闭宽海湾,高潮时刻相同的点联成的线(称之为等潮时线)绕无潮点反时针方向偏转。
2.潮流 宽海湾的潮流可视为两个相互垂直、位相相差π/2的驻波潮流的叠加,参照式(7—27)可知叠加后的潮流为:

7.5.5各种形态海区中潮波特性的比较
为了更好地理解各种形态海区中潮波的特性,表7—2作了一些比较。
由表可见,当潮波传入不同形态的海区,将有不同的波动形式,如果是窄长半封闭海湾,由于湾顶的反射将形成驻波;若在半封闭的宽海湾,因科氏力对潮波运动的影响不能忽略,潮波成为旋转潮波;当在长海峡中传播,由于地转效应也使潮波发生变形。在不同形态的海区,潮流、潮汐的变化规律往往有较大的差异,即使是相近的海区,潮差及潮时都可能不一样,潮汐动力理论对这些现象能给出很好的解释。
表7-2各种形态中潮波特性的比较(据文献)