前已提及,海洋中存在着各种不同周期的波动,对短波而言,例如风浪、涌浪只考虑重力对它们的作用,故称为重力波,地转效应可以忽略不计。但当波浪周期很大时,地转效应则不可忽视。一般认为当波动周期接近半摆日
![]()
6.5.1开尔文波
这是一种长周期重力波,即它同时受重力和科氏力的作用。因此它既具有重力波的基本特性,又在科氏力的作用下产生其他一些特点。
现讨论北半球的一列振幅为a的自由长波,当它通过一条无限长、具有侧向铅直边界,水深为h的水道时,在科氏力的作用下波动的情况。
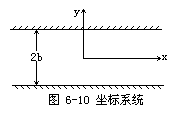
如图6—10所示,设水道的宽度为2b,x轴取在水道中央,y轴与水道垂直。波动以波速c沿x轴传播。求解波动方程(从略),其解的形式为
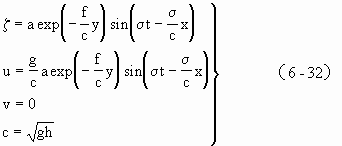
式中ζ为波面,显然它是x,y,t的函数,u,v为x与y方向上水质点
![]()
式(6-32)给出了开尔文波的基本特性。可见它是一种以波速
![]()
变化是同步的;由于水道的限制,故水质点在y方向上的速度分量v=0。它具有重力波的基本特性。但在重力波中,波动振幅为常量,而开尔文波的振幅却是y的函数。在水道的左岸(面向波浪传播方向),
![]()
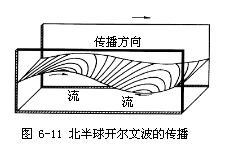
只在水道中央,即x轴上y=0处,其振幅为a。由上述可见水道左岸波动的振幅比右岸小。即波峰处,波面是右高左低,波谷处波面是左高右低(图6—11)。
不难理解,造成上述现象的原因正是由于科氏力作用的结果。由于u与ζ的变化是同步的,即|ζ|最大时,|u|也最大。当波峰到达时,ζ最高,u在x方向上也最大,此时在科氏力的作用下,海水向右岸堆积,导致海面自左岸向右岸上倾;当波谷到达时,ζ最低,u在x的负方向上最大,在科氏力的作用下,海水自右岸向左岸堆积,导致海面从右岸向左岸上倾。所以当波动通过水道时,水道两岸的波动振幅不等,右岸大,而左岸小。这是开尔文波的基本特征。对南半球而言恰好相反。
6.5.2罗斯贝波
罗斯贝波,亦称行星波,它是一种远远小于惯性频率f的低频波。它的
![]()
考虑β效应,求解波动方程得出的结论说明,它与前述波动具有一些基本不同的性质。
在密度均匀的海洋中,罗斯贝波具有以下频散关系:
σ=-βkx/K2 (6-33)
式中K为波数,反映波浪传播的方向,称为波数向量。它的三个分量分别为kx、ky、kz。由于我们讨论的波动只沿水平方向传播,故kz=0。因此
![]()
这样,沿波向及沿x、y方向的波速分量分别记为
![]()
因为K>kx,ky,所以,沿波向的波速c最小。将式(6-33),代入式(6-35),则得
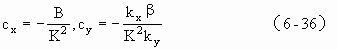
在我们取的坐标系中x向东,y向北,z向上,因此β值永远为正。K及其分量皆为实数,所以cx始终为负值,(cy为正或负则由ky决定),说明罗斯贝波的传播方向始终偏向西方。
![]()
其波速为0.16m/s。与相应的长重力波相比,小几个量级;其周期为14天,比相应的长重力波大好几个量级。
当波长很大时,罗斯贝波的频散关系具有如下形式
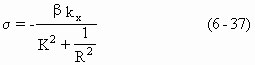
![]()
![]()
称为罗斯贝波形变半径。在中纬(45°)海域,水深h=500m的情况下,R=2.1×103km,若在10°的水域,则R=8×103km。
罗斯贝波的传播机制,可用位涡守恒的原理来解释。若海底平坦,则有位涡守恒
![]()
式中,ζ为相对涡度,f为行星涡度,二者之和为绝对涡度。显然当f增大时,ζ值为负,即产生顺时针旋转;反之,当f减小时,ζ值为正,产生逆时针旋转。用图6—12可以说明罗斯贝波传播的机制。
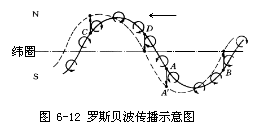
在图6-12中,设在参考纬圈上海水的相对涡度ζ为零,经过扰动,向北运动的海水,由于f值增大,据式(6—39),则ζ为负值,故产生顺时针的环流。同理,向南运动的海水,将产生逆时针方向的环流。且离开参考纬圈越远的海水涡度越大。可以设想,在实线上与D点相距无穷小的两点,所产生的环流将在D点相切,而偏北那点环流的南向分量要比偏南那点的向北分量大。因此在D点产生了一个净向南的分量。同理,在A点也产生一净向南的分量,在C,B两点产生净向北的分量。因此,下一时刻各点新位置的连线将如图中虚线所示,它表明罗斯贝波向西传播了。
由于罗斯贝波的波长很大,相比之下它在铅直方向上的运动十分微弱,在实际海洋中,可以认为它只是一种水平流系,流向基本与波向垂直。
海洋中还存在着许多长波运动形式,例如陆架波,它的特点是波动能量明显地集中在大陆架上沿海岸传播等等。本章不再作进一步介绍。
