200多年来,赞成日心说的天文学家们在恒星都很遥远的前提下,试图通过恒星视差的测量求出某些较近恒星的距离,但一直未能如愿以偿。这是很令人深思的。由这些天文学家的不懈努力所取得的有关天文成果一再表明,恒星视差测量这个看似简单的问题其实具有多种复杂因素。
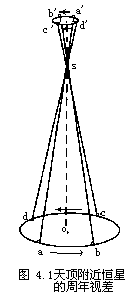
首先是望远镜的分辨率问题。地球绕太阳公转的轨道可以近似地看作圆轨道,如图4.1所示。在一年内地球沿该轨道abcd 运行一周,从而地球上所看到的天顶附近恒星S的投影位置也应当近似地描绘出圆轨道a′b′c′d′。由此可知圆轨道的角半径就等于该恒星S相对于日地基线oa的张角π,π亦称周年视差。则恒星S至地球的距离D可由下式求得:
![]()
式中r日地代表日地平均距离。因为π角很小,可用π代替sinπ;取r日地=1,并以角秒表示角度,可得:
![]()
既然许多代天文学家用望远镜也未能测出恒星的周年视差,那么一个重要原因必然是视差角π″小于望远镜可能分辨的最小角度。虽然增大望远镜物镜的直径可使极限分辨率提高到能测准小于1角秒(1″)的角度,但由于地球大气的折射和湍动诸因素所引起的非均匀效应,也会使大望远镜的实际分辨率达不到它的衍射极限。这就要求首先测出既离我们很近又位于天顶附近区域的恒星的视差。因为邻近恒星的视差角较大,而从天顶附近区域传来的星光则受大气的影响较小。
更有甚者,与地面上传统的三角测量不同,天文上对恒星视差π的测量,所用到的三角形aSo 是随时变化的。造成这种变化的原因既有目标S运动的因素,也有处于基线一端的测量点a运动的因素。前者要求测出恒星的自行并加以扣除,后者则要求测出地球公转运动所引起的光行差并加以扣除。显然,只有排除了所有的困难和障碍以后,才能最终测出微小的恒星视差。
德国天文学家贝塞耳(F.W.Bessel)正是基于上述多种考虑并经过多年努力,才于公元1838年第一个宣布测到一颗名叫天鹅座61的恒星视差为0.31角秒。在大致相同的时候,英国的亨德森(T.Henderson)和俄国的斯特鲁维也分别测得了半人马座α与织女星的视差。
考虑到视差位移方法的测量误差约为0.01角秒,贝塞耳测得天鹅座61的视差值0.31角秒,同现代所测得的值0.29角秒是相当接近的。这意味着该星与地球的距离是日地距离的710 000倍,即1.06×1014km。光从该星传到我们这里需要大约11年的时间,而太阳光传到我们这里只需8分多钟。可见恒星的距离是多么遥远,而能用三角测量法测得距离的恒星不过是少数视差大于0.01角秒的邻近的恒星。总之,这一扩大天文视野的成果虽然来之不易,但还是远远不够的。
