第四节 赫罗图
恒星作为一种光源也同其它许多光源(如灯光)类似,我们需要知道它们的最重要的观测性质,一个是发光强度,另一个则是主要发光颜色。恒星的主要发光颜色代表恒星的表面温度,如前所述,可以通过测得的恒星光谱型来确定;而恒星的发光强度,即光度,代表恒星的总辐射功率,则应当通过光度测量的步骤来确定。
由于恒星距离我们都很遥远,即使是很近的恒星,其真实圆面相对于观测点的张角也不过千分之几角秒,一般望远镜是分辨不清的。因此,正常的恒星都可以看作点源,而且该点源的辐射也可以看作各向同性的。假设用某种方法(如三角测量法)能够知道恒星的距离r,而且知道在该距离处恒星投来的单位面积上的辐射功率(即恒星的辐射流量密度)为F,则可立即求出该恒星的光度(总辐射功率)L:
L=4πr2F (4.5)
恒星的辐射流量密度F,可以根据落到望远镜孔径面上的辐射功率大小准确地测出,如果恒星的距离r也能准确地测出,则恒星的光度L就可以作为恒星的一个重要观测性质较好地确定下来。
两颗星的星等差m2-m1,同它们的辐射流量比F1/F2存在以下简单关系:
![]()
作为示例,已知太阳的视星等m2=m0=-26.73,从地球上直接测量的平均太阳辐射流量密度(太阳常数)F2=F0=0.137J/cm2·s;如果还知道另一颗恒星的视星等m1=20,则不难由(4.6) 式求得该恒星的辐射流量密度F1=3×10-20J/cm2· s。可见F1<<F0。但该恒星的光度是否也比太阳的光度小,则要由(4.5) 式中恒星距离r的大小来决定。设该恒星的距离是100秒差距(1秒差距=3.26光年=3.085×1018cm),则它的光度L1=3×1022J/s, 只比已知的太阳光度L0=4×1026J/s弱1万多倍。[NextPage]
(4.5)式表明,光度L一定的恒星,其辐射流量密度F同它的距离r的平方成反比,由(4.6)式导出的视星等m因而也同距离r有关,都不足以唯一地确定恒星的光度L,只有消去了距离影响的所谓绝对星等M才可与恒星的光度等效。这里的绝对星等M就是把所研究的恒星放到10秒差距的标准距离上应有的视星等。如果恒星在距离为r时的视星等为m,则它的绝对星等M可表示为:
M=m+5-5logr (4.7)
其中r以秒差距为单位。
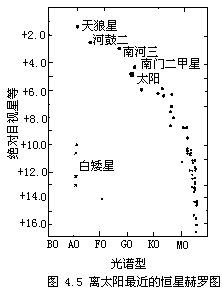
在望远镜的视场里,往往有许许多多的恒星,而且每颗恒星的两个最重要性质——光度L(即绝对星等M)和光谱型(即表面温度),都可以相当准确地由测量得知。这里提出的一个重要问题是:恒星的这两个性质是否彼此无关? 20世纪初,丹麦天文学家赫兹普隆(E. Hertzsprung)和美国天文学家罗素(H.N.Russell)各自独立进行的开创性工作便清楚地表明,恒星的光度与其光谱型是有密切关系的。后来,凡是描述这种关系的图形便均以赫罗图命名。
图4.5是离太阳5秒差距(16.3光年)以内恒星的赫罗图。沿横轴标示光谱型,沿纵轴标示绝对星等。图中某点的纵横坐标分别对应某颗恒星的绝对星等和光谱型。由图可见,各个点都不是随机分布的,而是按确定的星序分布的。大多数恒星都聚集在一条相当窄的带内,该条带自图的左上角一直延伸到右下角,称为主星序;处于主星序的恒星则称为主序星。在主星序内,恒星的光谱型逐渐从B变到M,相应的恒星表面温度也逐渐从高变到低。 在主星序外的左下方,还有5颗星,颜色发白但光度小(绝对星等在10以上),称为白矮星。
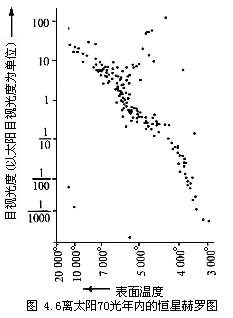
当我们把观测范围再扩大些,例如扩大到离太阳70光年以内的有关恒星,则会得到包含更多恒星的赫罗图,如图4.6所示。这里横轴标示表面温度(以绝对温度K为单位),纵轴标示光度(以太阳的目视光度为单位)。由图可见,大多数恒星仍然落在主星序条带内,在主星序外的左下方,也有几颗白矮星。此外,主星序外的右上方新增加了一些图4.5所没有的星,它们颜色发红、光度大,称为红巨星。
由于表面温度为T的恒星的辐射近似于相同温度的黑体的辐射,所以,整个恒星表面的辐射功率(即光度L)可以表示为:
L=4πR2·σT4 (4.8)
其中斯忒藩-玻耳兹曼常数σ=5.67×10-8W/m2·K4,R是恒星的半径。因此,要求得恒星的半径R,就必须知道它的光度L和表面温度T。用(4.8)式分析图4.6可知,同有关主序星相比,有相同高表面温度T的恒星,如果光度L小则必然半径R也小,故称为白矮星;而有相同低表面温度T的恒星,如果光度L大则必然半径R也大,故称为红巨星。恒星半径这个光学望远镜本来“望尘莫及”的参量,竟然在这里自然地被导出,这不能不说是物理理论与天文观测相结合的一项重要成果。
在主星序内,恒星的另一个重要参量——质量同它的光度也是有一定关系的。不过,能可靠地测出质量的恒星是不多的。如果两颗星构成双星,并且知道它们相互绕转的轨道半长轴和周期,则子星的质量可由开普勒第三定律较为精确地求得。这类似于通过行星的运动定出太阳质量的方法。而对于没有伴星的单一恒星,则只好心照不宣地默认,光度和颜色都相同的恒星具有相同的质量。在恒星质量m已知的情况下,则可由以下质光关系式定出其光度L(反之亦然):

式中L0、M⊙分别是太阳的光度和质量,μ和H则分别是恒星物质的平均分子量和不透明度。该式表明,恒星的光度L与恒星的半径无关,但与它的质量的三次方成正比。这也意味着越靠近赫罗图主星序条带左上方的恒星,它的质量就越大,如图4.7所示。

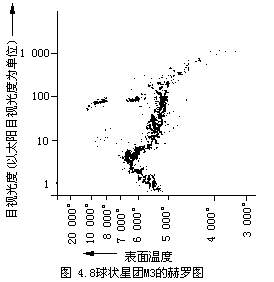
图4.8是猎犬座中球状星团M3的赫罗图。图中大多数光度大的恒星都不是主序星。为什么在一般赫罗图中绝大多数恒星都是主序星而该图却并非如此呢?是否高光度、大质量的恒星因能量消耗大而不能长久地停留在主星序阶段?红巨星和白矮星又是属于哪个阶段的恒星?恒星是怎样诞生的?恒星的最终结局又是怎样?这些都是恒星演化的重大课题。如果没有通过大量天文观测研究取得恒星的赫罗图,这些问题是不会从科学的角度提出来的,当然就更谈不上去解决了。赫罗图的重大研究意义从这里也就可想而知了。