第七节 典型叠加模型的分析
三、模糊逻辑方法
1.概 述
在古典集合论中,集合的成员被定义为真值(True)或假值(False),即0或1。但是,对于一个模糊集合来说,它的成员可以用从1到0的一个连续尺度来表达。下面是一个基于模糊集合成员的函数关系例子:
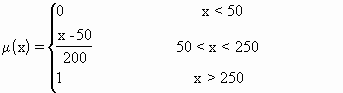
这里,假设x是某个元素的浓度值水平,μ(x)是一个模糊关系函数。x的每一个值都有一个μ(x)值,而一系列的有序对[x,μ(x)]就组成了一个模糊集合。模糊关系函数曲线的形状可以不是线性的,它可以表现为任何问题研究所要求的或者主观设计所希望的形状(如图4.32)。模糊关系函数也可以用表格的形式来表达,例如,对于有关某个元素的浓度值分布的模糊关系函数,可以用表4.6(级别间格为50个波度单位)的离散数据形式来表达,它与上面函数关系的分析表达形式效果相同。
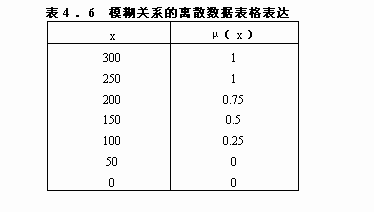
在属性表中,图层的各个数据级别都与模糊关系值相连系。而图层的数据级别的分级方式包括等间格或不等间格的分级,但模糊关系值则必须位于[0,1]范围。模糊关系值的确定是基于人的主观判断,以反映集合成员的重要性程度为目的而进行的。
与图层权重和数据级别分数一样,模糊关系值实质上反映了每一数据层对于问题解决的重要性程度以及同一数据层内不同数据级别的相对重要性。
