第六节 板块运动
在讨论板块的球面运动时,通常认为板块是刚性或近于刚性的,并认为地球表面积保持不变,这样就有可能用数学方法来描绘板块运动了。
板块相对运动及其几何学
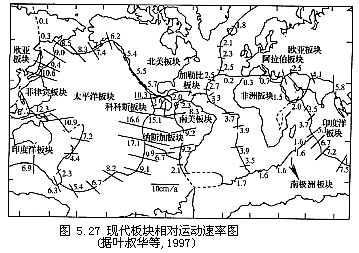
板块运动一般是指地球表面一个板块对于另一个板块的相对运动。举例来说,大西洋中脊两侧的欧亚板块和北美板块正在相互分离,但这并不能断定大西洋中脊相对于地理极是静止的,也无法确定两个板块之中哪一个是静止不动的,我们只能假定其中一个板块静止不动,然后去分析另一板块相对于它的运动。由此可知,欧亚板块相对于北美板块是向东运动,而北美板块相对于欧亚板块则是向西运动。欧亚板块相对于太平洋板块是向西运动,相对于印度洋板块则是向南运动。举例说来,大西洋四周各大陆间的距离,在过去2亿年的时间内,至少移动了数千千米,而利用现代空间技术所观测到的现代板块间的相对运动,则可以达到每年几个厘米的量级(图5.27)。
刚体板块沿地球表面的运动,应遵循球面运动原理,即必定是环绕通过球心(地心)轴的旋转运动(图5.28)。在球面上,任何一点的移动都不是沿着直线而是沿着弧线的运动。平行于赤道(离旋转极90°的大圆)的一系列同轴圆弧(欧拉纬线)标明了板块旋转运动的方向,同轴圆弧的垂线(大圆)相交于旋转极。正因为板块运动是一种旋转运动,所以,板块上不同位置的线速度随远离旋转极而增大,至旋转赤道线速度最大。板块的旋转运动由旋转极(欧拉极、扩张极)的地理坐标(γ、 )和旋转角速度(ω)确定。
![]()
![]()
界上一些点的相对速度和方向,也可反演两板块间相对运动的欧拉矢量。

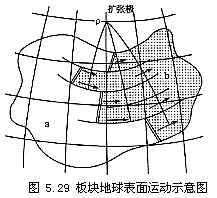
由于转换断层的走向平行于相邻板块之间的相对运动方向,也就是说,相邻板块在球面上的运动轨迹就是转换断层(图5.29),故采用求转换断层为界的各对板块之间相对运动的旋转极(ρ),例如,采用作图法对大西洋中脊不同转换断层分别作垂直于它们的球面大圆,结果都相交于球面上一个很小的范围内,理解为一个极点,即旋转极,实际位置在58°E及38°W附近。
有了扩张极(旋转极),利用扩张速率便可求出旋转角速度,即:ω=ν/R·cosθ·0.017 45式中ω为旋转角速度(度/a);ν为扩张速率(cm/a); R为地球半径(6.37×108cm); θ为欧拉纬度; 0.017 45为角度的弧长系数。表5.2即为明斯特(J.B.Minster etal, 1974)和蔡斯(C.Chase 1978)等人求出的全球部分板块之间现代运动的扩张极和角速度,根据所求得的旋转极位置和角速度大小,板块边界上各点的线速度可以很方便地换算出来。
表5.2 全球部分板块的旋转及旋转速度
|
相对旋转的板块对 |
旋转极坐标 |
旋转角速度 (10-7度a) |
|
|
纬度 |
经度 |
||
|
欧亚—非洲/29.6N |
25.7W |
1.4 |
|
|
29.2N |
23.5W |
1.42 |
|
|
欧亚—印度 |
23.0N |
33.9E |
6.5 |
|
24.2N |
37.4E |
7.17 |
|
|
欧亚—太平洋 |
65.3N |
69.9W |
9.1 |
|
60.8N |
80.6W |
9.5 |
|
|
印度—太平洋 |
59.8S |
178.0E |
12.6 |
|
62.0S |
174.3E |
12.72 |
|
|
印度—南极洲 |
10.7N |
31.6F |
6.7 |
|
17.4N |
32.1E |
6.79 |
|
|
太平洋—南极洲 |
68.7N |
79.6W |
10.3 |
|
66.2N |
83.5W |
10.05 |
|
|
太平洋—纳兹卡 |
56.6N |
85.6W |
16.4 |
|
50.9N |
87.0W |
16.85 |
|
|
北美—太平洋 |
50.9N |
66.3W |
7.5 |
|
48.2N |
72.3W |
8.64 |
|
|
太平洋—菲律宾海 |
45.5N |
150.2E |
12.0 |
|
39.5N |
141.7E |
8.73 |
|
|
北美—欧亚 |
69.3N |
128.0E |
2.7 |
|
53.7N |
137.3W |
2.29 |
|
由前述可知,当两个各具边界形态的板块发生运动时,它们都有自己的旋转轴及旋转极,若三个板块同时发生运动则它们三者不可能是绕同一旋转极的转动,其中第三个板块的旋转极必然随转动而移动变位,所以,其旋转极只能是一个平均数。另外,每对板块扩张极的位置在时间上是变化的,所以,板块运动的旋转极只具有瞬时的位置性质。判断板块运动的标尺是时间段落,所以,旋转极就总是一个平均数,空间上是一个理想的点。对重建古大陆位置而言,确定板块旋转极的位置非常重要。
