第三节 大气的水平运动和垂直运动

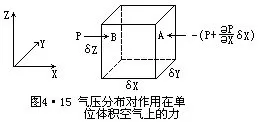
空气的运动是在力的作用下产生的。作用于空气的力除重力之外，尚有由于气压分布不均而产生的气压梯度力，由于地球自转而产生的地转偏向力，由于空气层之间、空气与地面之间存在相对运动而产生的摩擦力，由于空气作曲线运动时产生的惯性离心力。这些力在水平分量之间的不同组合，构成了不同形式的大气水平运动。

（一）气压梯度力

气压梯度是一个向量，它垂直于等压面，由高压指向低压，数值等于两等压面间的气压差（△P）除以其间的垂直距离（△N），用下式表达：

式中G_N为气压梯度，由于△N是从高压指向低压，△P为负值，故

经度相差一度的纬圈长度，其值约为111km）。观测表明，水平气压梯度值很小，一般为1—3hPa/赤道度，而垂直气压梯度在大气低层可达1/10m左右，即相当于水平气压梯度的10万倍，因而气压梯度的方向几乎与垂直气压梯度方向一致，等压面近似水平。

气压梯度不仅表示气压分布的不均匀程度，而且还表示了由于气压分布不均而作用在单位体积空气上的压力。为了阐明这个问题，在气柱的P和P＋δP间取一小块立方体流体（图4·15），其体积是δV=δXδYδZ， Y轴平行于地面等压线， X轴指向较高气压方向， Z轴垂直向上，并与地面重力作用线平行。

立方体周围空气对气块B面施加的压力等于PδXδZ（P是这个面上

号是因所取压强方向与X方向相反），因而在X方向上，周围空气作用于立方体的净压力为此两力之和，即

所以气压梯度是作用于单位体积空气上的力。

实际大气中，由于空气密度分布的不均匀，单位体积空气块质量也是不等的。根据牛顿第二定律，在相同的气压梯度力作用下，对于密度不同的空气所产生的运动加速度是不同的，密度小的空气所产生的运动加速度比较大，密度大的空气所产生的运动加速度比较小。因此，用气压梯度难以比较各地空气运动的速度。在气象上讨论空气水平运动时，通常取单位质量的空气作为讨论对象，并把在气压梯度存在时，单位质量空气所受的力称为气压梯度

式中ρ是空气密度，△P是两等压面间的气压差，△N是两等压面间的垂直距离。气压梯度力的方向由高压指向低压，其大小与气压梯度-△P成正比，与空气密度ρ成反比。气压梯度力可以分解为水平气压梯度力（G_n）和垂直气压梯度力（G_z），即：

在大气中气压梯度力垂直分量比水平分量大得多，但是重力与G_z始终处于平衡状态，因而在垂直方向上一般不会造成强大的垂直加速度。而水平气压梯度力虽小，由于没有其它实质力与它相平衡，在一定条件下却能造成较大的空气水平运动。

通常，在同一水平面上，密度随时间、地点变化不很明显，因此水平气

梯度力相比较时，ρ的差异才需要考虑。实际大气中经常出现的数据是：ρ

这种气压梯度力持续作用3h，可使风速由零增大到7.6m/s。可见气压梯度力是空气产生水平运动的直接原因和动力。 

（二）地转偏向力

空气是在转动着的地球上运动着，当运动的空气质点依其惯性沿着水平气压梯度力方向运动时，对于站在地球表面的观察者看来，空气质点却受着一个使其偏离气压梯度力方向的力的作用，这种因地球绕自身轴转动而产生的非惯性力称为水平地转偏向力或科里奥利力。在大尺度的空气运动中，地转偏向力是一个非常重要的力。

为了阐明地球自转产生偏向力的原因，先做一个实验。取一个圆盘并让它作逆时针旋转（图4·16），同时取一小球让它从圆盘中心O点向OB方向滚去。水平方向上如果没有外力作用于小球，则小球保持着惯性沿OB直线匀速地滚动着，圆盘的转动对小球运动的方向和速度都没有影响。但当小球自O点沿OB方向滚动到圆盘边缘的时间里，站在圆盘上A点的人也随圆盘一起转动，并由A移到A'位置上。如观察者以其立足的圆盘作为衡量物体运动的参照标准，在他看来，小球并没有作直线运动向他滚来，而是作曲线运动向右（沿小球运动方向看）偏移到A的位置上了，如图4·16中虚线所示。按牛顿运动定律，这种看来向右偏转。好像是小球在作直线运动时，时刻受到的一个同它运动方向相垂直并指向其右方的作用力，就是由于圆盘转动所产生的偏向力，也就是随圆盘一起转动的观察者所观察到的力。这种力是假想的，事实上并无任何物体作用于小球来产生这个力，只是为了要在一个非惯性系里以牛顿定律来解释所观察到的现象而引进的一个假想力。

为了计算由地转偏向力所引起的相对加速度α，假设小球运动的速度是V，从O点出发经过时间t到达A点，它的位移为OA=Vt。与此同时，圆盘逆时针转动了角∠AOA'，圆盘转动的角速度为ω，在t秒钟内转过的角度∠AOA'=ωt。以 S表示小球偏离的距离，并且近似等于，如略去其差别，则S==OA×∠AOA'，

以OA=Vt，∠AOA'=ωt代入上式，则S=Vωt²，

圆盘上偏向力表达式表明，A的大小等于圆盘的角速度ω与小球运动速度V的乘积的两倍。A的方向垂直于转动轴，也垂直于相对速度V，指向V的右侧。

地球不停地绕地轴以角速度ω从西向东自转，生活在地球上的人和上述圆盘上的人很相似会很自然地以转动的地表作为衡量物体运动的标准，所不同的是转动的球体表面更为复杂。然而圆盘非常相似地球极点的地平面。

在北极，地平面绕其垂直轴（地轴）的角速度恰好等于地球自转的角速度ω。转动方向也是逆时针的。因而在北极，单位质量空气受到的水平地转偏向力与空气运动方向垂直，并指向它的右方，大小等于2Vω。

在赤道，地球自转轴与地表面的垂直轴正交，表明赤道上的地平面不随地球自转而旋转，因而赤道上没有水平地转偏向力。

在北半球的其它纬度上，地球自转轴与地平面垂直轴的交角小于90°，因而任何一地的地平面都有绕地轴转动的角速度。见图 4·17，图上ω表示绕地轴转动的角速度，AC表示A点地平面的垂直轴。由于∠AOD=φ，所以∠ABC=φ，ω在地平面垂直轴方向的分量为ω₁（ωsinφ）。根据圆盘转动速度所得的公式α=2Vω，可以得出任何纬度上作用于单位质量运动空气上的偏向力为：

A=2Vωsinφ

在南半球，由于地平面绕地轴按顺时针方向转动，因而地转偏向力指向运动物体的左方，其大小与北半球同纬度上的地转偏向力相等。

地转偏向力只是在空气相对于地面有运动时才产生，空气处于静止状态时没有地转偏向力作用。而且地转偏向力只改变气块运动方向而不能改变其运动速度。在风速相同情况下它随纬度减小而减小。见表4·3。

（三）惯性离心力

惯性离心力是物体在作曲线运动时所产生的，由运动轨迹的曲率中心沿曲率半径向外作用在物体上的力。这个力是物体为保持沿惯性方向运动而产生的，因而称惯性离心力。惯性离心力同运动的方向相垂直，自曲率中心指向外缘（图4·18），其大小同物体转动的角速度ω的平方和曲率半径r

（4·10）式表明惯性离心力C的大小与运动物体的线速度V的平方成正比，与曲率半径r成反比。

实际上，空气运动路径的曲率半径一般都很大，从几十千米到上千千米，因而空气运动时所受到的惯性离心力一般比较小，往往小于地转偏向力。但是在低纬度地区或空气运动速度很大而曲率半径很小时，也可以达到较大的数值并有可能超过地转偏向力。

惯性离心力和地转偏向力一样只改变物体运动的方向，不改变运动的速度。 

（四）摩擦力

是两个相互接触的物体作相对运动时，接触面之间所产生的一种阻碍物体运动的力。大气运动中所受到的摩擦力一般分为内摩擦力和外摩擦力。

内摩擦力是在速度不同或方向不同的相互接触的两个空气层之间产生的一种相互牵制的力，它主要通过湍流交换作用使气流速度发生改变，也称湍流摩擦力。其数值很小，往往不予考虑。

外摩擦力是空气贴近下垫面运动时，下垫面对空气运动的阻力。它的方向与空气运动方向相反，大小与空气运动的速度和摩擦系数成正比，其公式为

R=-kV               （4·11）

式中R为摩擦力，k为摩擦系数，V为空气运动速度。内摩擦力与外摩擦力的向量和称摩擦力。摩擦力的大小在大气中的各个不同高度上是不同的，以近地面层（地面至30—50m）最为显著，高度愈高，作用愈弱，到1—2km以上，摩擦力的影响可以忽略不计。所以，把此高度以下的气层称为摩擦层（或行星边界层），此层以上称为自由大气层。

上述四个力都是在水平方向上作用于空气的力，它们对空气运动的影响是不一样的。一般来说，气压梯度力是使空气产生运动的直接动力，是最基本的力。其它力是在空气开始运动后产生和起作用的，而且所起的作用视具体情况而有不同。地转偏向力对高纬地区或大尺度的空气运动影响较大，而对低纬地区特别是赤道附近的空气运动，影响甚小。惯性离心力是在空气作曲线运动时起作用，而在空气运动近于直线时，可以忽略不计。摩擦力在摩擦层中起作用，而对自由大气中的空气运动也不予考虑。地转偏向力、惯性离心力和摩擦力虽然不能使空气由静止状态转变为运动状态，但却能影响运动的方向和速度。气压梯度力和重力既可改变空气运动状态，又可使空气由静止状态转变为运动状态。

（五）大气运动方程

大气运动方程是描述作用于空气微团上的力与其所产生的加速度之间关系的方程。根据牛顿第二定律，物体所受的力等于质量和加速度的乘积，即F=ma，F为物体所受的力，是各个作用力的总和。单位质量空气运动方程的一般形式为

以FX、FY、FZ分别表示作用力在标准坐标系 X、Y、Z三个方向（X指向东、Y指向北、Z指向天顶）上的投影，则

式中u、v、w分别为V在X、Y、Z三个方向上的分量。

将G、A、R、g值代入上式，简化后的运动方程为

在空气作大规模水平运动中，大气近似于静力平衡，因而上式中的垂直运动项可以略去。在自由大气中，R也可略去。上式可写成

这是研究自由大气运动时被广泛应用的运动方程式。方程中第三式是静力平衡方程。