在水平压强梯度力的作用下,海水将在受力的方向上产生运动。与此同时科氏力便相应起作用,不断地改变海水流动的方向,直至水平压强梯度力与科氏力大小相等方向相反取得平衡时,海水的流动便达到稳定状态。若不考虑海水的湍应力和其它能够影响海水流动的因素,则这种水平压强梯度力与科氏力取得平衡时的定常流动,称为地转流。
5.3.1地转方程及其解
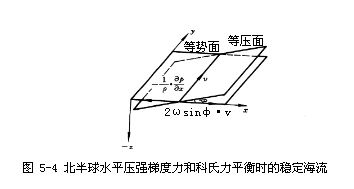
为讨论简便起见,设等压面只沿直角坐标系的x轴方向倾斜,它与等势面的夹角为β,如图5-4所示。此时海水运动方程简化为
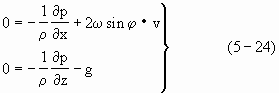
第二式即为静力方程。由第一式直接可得
![]()
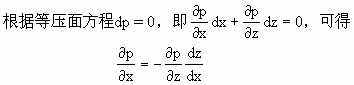
由式(5-24)可得
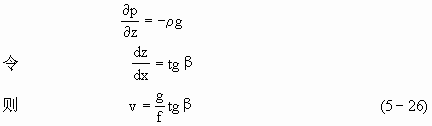
式(5—26)给出了上述特殊情况下的地转流速公式。它与等压面倾角
![]()
而f=0,故式(5—26)不适用于此处。
上述情况下,地转流向沿y轴方向,且在等压面与等势面的交线上流动。在北半球垂直于压强梯度力指向右方,当观测者顺流而立时,右侧等压面高,左侧低。即等压面自左下方向右上方倾斜。在南半球则与之相反。
在整个海洋中由内压场与外压场导致的地转流却具有其特定的分布形式。由内压场导致之地转流,一般随深度的增加流速逐步减小,直到等压面与等势面平行的深度上流速为零;其流向也不尽相同,有时称其为密度流。由外压场导致的地转流,自表层至海底(除海底摩擦层外),流速流向相同,有时称其为倾斜流。然而在实际海洋中,地转流往往是在总压场作用下引起的。
5.3.2地转流场与密度场、质量场之间的关系
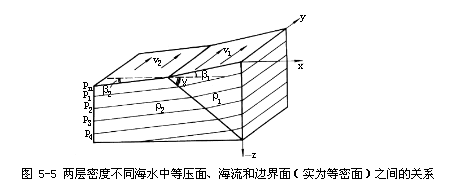
海洋中的密度变化是连续的,因此,由于海水密度分布不均匀产生斜压场引起的地转流场的变化也应当是连续的。但为了简便起见,仅取两层密度不同的海水加以讨论。设上下层海水密度分别为ρ1与ρ2,且ρ2>ρ1。在海水静止时,其界面应是水平的。然而当上下层海水分别以流速v1与v2流动时,则界面一般不会再是水平的,而会发生倾斜,设其相对x轴的倾角为γ。另外设等压面也只在x轴方向倾斜,上下两层海水等压面的倾角分别为β1与β2。海水只在y轴方向流动,如图5—5所示。
通过两层海水界面时海水的压力变化是连续的,界面上任意两点之间的压力差为dp,即有
dp1=dp2
![]()
![]()
![]()
![]()
![]()

此式可应用于密度连续变化的海洋中。
式(5—28)和(5—29)两式给出了密度界面(在密度连续变化的海洋中为等密度面)的倾角与流场、压力场之间的相互关系。可见只有在ρ2v2=ρ1v1,即上下两层海水的动量相等时,界面才是水平的,这在海洋中,特别是大洋上层一般难以满足,因为等密度面通常是倾斜的。不过在赤道例外,因为那里f=0,所以tgγ=0。
等密度面的倾角比等压面的倾角大得多,一般为等压面倾角的102~103倍。这就为利用密度场描述地转流提供了方便条件。
实际海洋中的地转流流速,一般是上层大于下层,不难从式(5—29)中看出,设v2=0,
![]()
因为ρ2>ρ1,故上式永远为负值,即tgβ1与tgγ符号相反,说明等压面与等密面相对x轴倾斜方向相反。反之,当上层流速小于下层流速时,则等压面与等密面的倾斜方向相同。但这在海洋中比较少见。
上述关系可用下述法则综合:当上层流速大于下层流速时,我们顺流而立,则在北半球密度小的海水在右侧,密度大的海水在左侧,等压面自左向右上倾斜。在南半球则相反。
海水密度,特别在大洋上层,其水平分布主要由温盐决定,因此等密面的倾斜方向通常与等温面和等盐面的倾斜方向相同,从而与等压面的倾斜方向相反。实际工作中常常可以根据等温面(线)或等盐面(线)的倾斜方向定性地推知地转流的方向。
