小振幅重力波,亦称正弦波,是一种简单波动。简单波动的特性可近似地说明实际海洋波动的许多现象。小振幅重力波系指波动振幅相对波长为无限小,重力是其唯一外力的简单海面波动。
理论上解决的办法是:根据流体力学的连续方程、运动方程和边界条件,在假定流体无粘滞性,运动是无旋的,波面上的压力为常数的条件下求解。本章只引用已有理论的结论,着重于一些基本概念的论述。以下就小振幅波动的波形传播与水质点的运动、波速、周期与波长的关系,波动能量,波动的叠加等问题加以讨论。
6.2.1波形传播与水质点的运动
取右手直角坐标系,z轴向上为正,将x—y平面放在海面上,设波动是二维的,只在x方向上传播,则波剖面方程可用下列正弦曲线表示,即:
ζ=αsin(kx-σt) (6-1)
式中α为波动的振幅,ζ为波面相对平均水面的铅直位移。显然它是地点x与时间t的函数,式中
![]()
分别称为波数和频率。当水深为h时,可证明它们的关系为
σ2=kgtanh(kh)=kgtanh(2πh/λ)① (6-2)
称为频散关系。式中g为重力加速度。
由式(6-1)可见,当(kx-σt)=π/2时,ζ=a,即为波峰。相速为
![]()
亦即
![]()
波形向前传播完全是由水质点的运动而产生的,但是它们二者却绝非一回事。正如麦田中麦浪滚滚向前,而麦株并不向前运动的道理一样。
若水深h大于波长的一半(h/λ≥0.5),此时的波动称为深水波或者短波。可以证明水质点在x与z方向上的速度分量u,w分别为

可见,在水平方向与铅直方向上的速度分量都是周期性变化的,且随深度增加(-z)而指数减小。在自由表面,水质点的速度分量为
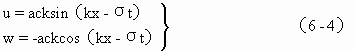
由于小振幅波中假定其振幅相对波长无限小,因此水质点的运动路程极短,故式(6-3)中水质点的实际坐标(x,z)可近似地以其平衡位置(x0,z0)代替。从而得到

对以上两式积分后,两边平方相加,消去t得
(x-x0)2+(z-z0)2=a2exp(2kZ0) (6-6)
说明水质点的运动轨迹为圆,半径为aexp(kZ0),轨迹半径随深度的增大(z<0)迅速减小。在自由表面z0=0,其半径为其振幅a,当深度增大至
![]()
已可忽略不计。
比较(6-1)与(6-3),不难看出,水质点在波峰处(kx-σ
![]()
最大水平速度,且其铅直速度分量w皆为零。处在平均水面上的水质点,水平速度分量皆为零。铅直速度分量最大。而且波峰前部为正(向上),波峰后部为负(向下)。因此,波峰前部为水质点的辐聚区,波面未来上升,而波峰后部则为辐散区,未来波面下降,从而使波形不断向前传播,而水质点却只围绕自己的平衡位置作圆周运动,见图6-3。

深水波中,无论水质点的运动速度还是轨迹半径(从而波高)都随深度的增大而呈指数减小。当到达一个波长的深度时波动已近消失。
![]()
波。长波中水质点的运动轨迹为椭圆,随深度的增加椭圆长轴几乎不变,而短轴迅速减小,近海底处几乎只在水平方向上作周期性往复运动。
值得提出的是,无论长波还是短波,尽管它们的水质点运动轨迹不同,但是随深度(-z)的增大,它们的波长λ是不变的,即在自由水面的波长多大,随深度增大直至波动消失处的波长仍为多大。
![]()
→x,当x→∞,tanhx→1
6.2.2波动公式与波动能量
一、波速、波长与周期公式
(一)波速与波长的关系将频散关系式σ2=kgtanh(kh)代入
![]()

(二)波长与周期的关系
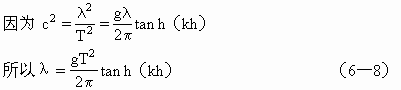
(三)波速与周期的关系

式(6—7)(6—8)(6—9)是波速、波长、周期之间的普遍关系,对长波与短波都适用。
![]()
=0.99626≈1,因此
![]()
![]()
![]()

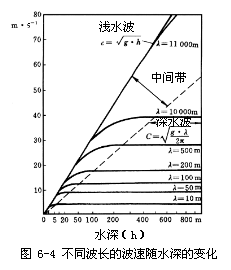
可见对深水波而言,其波速与水深无关,仅与波长有关,对长波而言则与波长无关而只与水深h有关。
当相对水深h/λ界于1/2与1/20之间时,则必须考虑浅水订正项tanh(kh)。图6—4给出了不同波长的波速随水深h的变化情况。
二、波动的能量
波动具有巨大的能量。波动中水质点的运动产生动能,而波面相对平均水面的铅直位移则使其具有势能。
对于小振幅波不难证明,单位截面铅直水柱内的势能为
![]()
沿波峰线单位宽度一个波长内的势能
![]()
式中ρ为海水密度,H为波高。
取波峰线方向单位宽度,自表至波动消失处(深水波),一个波长所具有的动能为
![]()
可见在一个波长内,波动的势能与动能相等,其总能量为
![]()
它与波高的平方成正比,即波动的能量以波高的平方增长。在讨论波动的能量时,常以波高的平方作为能量的相对尺度。以上指的是波动的总能量,至于能量的时空分布,在海水内部却是不断变化的。事实上,由于波动随深度的迅速减小,因此总能量主要集中在水面附近。在这种意义上称这种波动为表面波。
波动的能量沿波浪传播万向不断向前传递,在平均的意义下其传递速率为
![]()
即波动的总能量以半波速向前传递。
波动所具有的能量是相当可观的。例如波高为3m、周期为7s的一个波动,跨过10km宽的海面,其功率为63×104kW,海浪能量之大可见一斑。
三、正弦波的叠加
实际海洋中的波动远非简单波动的上述性质能够加以描述。例如,在陡峭的海岸、码头附近和港湾内,由于波动的反射造成的驻波;在海洋中,波浪的传播往往是一群一群的,个别波动的振幅并不相等,且随时随地变化着等等。诸如上述情况可用简单波动的叠加加以解释。
(一)驻波
设有两列振幅、周期、波长相等,但传播方向相反的正弦波
ζ1=asin(kx-σt)和ζ2=asin(kx+σt)
叠加,合成后的波剖面方程为ζ=ζ1+ζ2,则
ζ=2acosσt·sinkx (6-16)
为方便起见,取下列几个特定时刻的波面加以讨论。由式(6—16)可见,当

![]()
波面具有最大的铅直升降,其值为2a,即合成前振幅的两倍,这些点称为波
![]()
称为波节。在波节与波腹之间的波面升降幅度均在0-2a之间。随着时间的
![]()
![]()
外传播,故称为驻波。波节处只有水质点的水平速度分量u,其方向指向波面上升的一侧。波腹处只有水质点的铅直运动分量w,与波面升降方向相同。波面上其他各点两种速度分量都存在。当波面上各点|ζ|值达到最大值时,此时u=w=0,而ζ=0时,u,w达到最大值。以上各点是驻波所具有的基本特点。
(二)波群
设两列振幅相等,波长与周期相近,传播方向相同的正弦波
ζ1=asin(kx-σt)和ζ2=asin(k'x-σ't)
叠加,其波剖面方程为ζ=ζ1+ζ2,则
![]()
上式表示合成后的波动以振幅
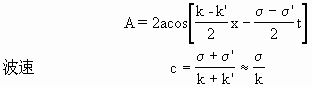
向前传播的波动,可见其传播速度与合成前简单波动速度相近,但其振幅A却仍然为x与t的函数,不断地周期性变化着,变化范围在0~2a之间,变化的速度为

图6—5为上述波动的剖面图。这种合成后的波动振幅由小到大(0→2a),又由大到小(2a→0)形成群集分布,故称为群。A即为群的包络线,显然cg就是群的传播速度,称为群速。

由关系式 σ2=kgtanh(kh)
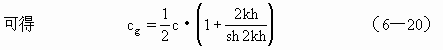
式中sh为双曲正弦符号。
对深水波而言,2kh/sh2kh=0,故
![]()
对浅水波,2kh/sh2kh≈1,故 cg=c
也就是说,深水波的群速为波速的一半。浅水波的群速与波速相等,群速也可视为波动能量的传递速度。
